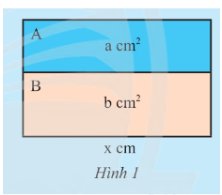
Một hình chữ nhật lớn được ghép bởi hai hình chữ nhật A và B lần lượt có diện tích là \(a\) \(c{m^2}\) và có cùng chiều dài \(x\) cm (Hình 1).
a) Tính chiều rộng của hình chữ nhật lớn theo hai cách khác nhau.
b) Chiều rộng của B lớn hơn chiều rộng của A bao nhiêu? Biết \(b > a\)


a) Cách 1: Chiều rộng hình chữ nhật lớn là: \(\left( {a + b} \right):x = \dfrac{{a + b}}{x}\) (cm)
Cách 2: Chiều rộng của hình chữ nhật A là: \(a:x = \dfrac{a}{x}\) (cm)
Chiều rộng của hình chữ nhật B là: \(b:x = \dfrac{b}{x}\) (cm)
Chiều rộng của hình chữ nhật lớn là: \(\dfrac{a}{x} + \dfrac{b}{x} = \dfrac{{a + b}}{x}\) (cm)
b) Chiều rộng của B lớn hơn chiều rộng của A là: \(\dfrac{a}{x} - \dfrac{b}{x} = \dfrac{{a - b}}{x}\) (cm)