Tính diện tích đáy của hình hộp chữ nhật có thể tích \(V = 12{x^2}y\) và chiều cao bằng \(3y\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2023
`a,` Chiều dài ` =(6xy+10y^2) : 2y = 3x + 5y`.
`b,` Diện tích đáy: `(12x^3 - 3xy^2 + 9x^2y) : 3x`
`= 4x^2 - y^2 + 3xy`
22 tháng 7 2023
Chiều cao của hình HCN đó là:
`(6x^2y - 8xy^2) \div 2xy`
`= 6x^2y \div 2xy - 8xy^2 \div 2xy`
`= 3x - 4y`
22 tháng 7 2023
Chiều cao là: `V : S = (6x^2y - 8xy^2) : 2xy = 3x - 4y`.
20 tháng 9 2023
Tham khảo:
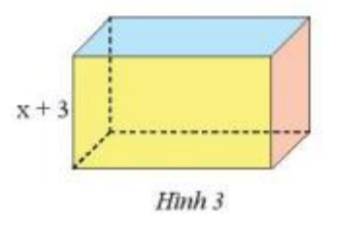
\( \Rightarrow ({x^3} + 8{x^2} + 19x + 12):(x + 3) =\) diện tích đáy
Ta có :
Vậy diện tích đáy là : \({x^2} + 5x + 4\) \(c{m^2}\)
TH
1 tháng 3 2022
Gọi cạnh của hình lập phương là a.
Thể tích của hình lập phương là : a × a × a.
Thể tích hình hộp chữ nhật là : 40 × 10 × a.
Ta có : a × a × a = 40 × 10 × a
a × a = 40 x 10 (chia cả hai phép tính cho a)
Vậy a × a = 2a = 400 ⇒ a = 20.
⇒ Cạnh hình lập phương là 6cm.
Diện tích xung quanh của hình hộp chữ nhật là:
( 40 + 10) x 2x 20 = 2000 (cm²)
Thể tích của hình lập phương:
20 × 20 × 20 = 8000 ( cm³ )
AH
Akai Haruma
Giáo viên
12 tháng 2 2022
Gọi chiều dài và chiều rộng hình hộp lần lượt là $a$ và $b$ (cm)
Theo bài ra ta có: $a\times b=36$
Diện tích xung quanh hình hộp chữ nhật: $12\times b\times 2+12\times a\times 2+a\times b\times 2$
$=24\times (a+b)+2\times a\times b=24\times (a+b)+2\times 36=72+24\times (a+b)$
Không tính được cụ thể. Bạn coi lại đề.
Diện tích đáy của hình hộp chữ nhật là:
\(S_{\text{đáy}}=\dfrac{V}{3y}=\dfrac{12x^2y}{3y}=4x^2\)