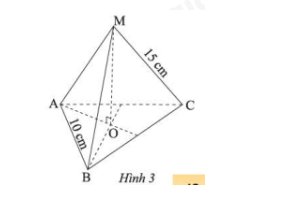
Hãy cho biết mặt bên, mặt đáy, đường cao, độ dài cạnh bên, độ dài cạnh đáy của hình chóp tam giác đều ở Hình 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
- Mặt bên: \(MAB\), \(MAC\), \(MBC\)
- Mặt đáy: \(ABC\)
- Đường cao: \(MO\)
- Độ dài cạnh bên: \(15\)cm
- Độ dài cạnh đáy: \(10\)cm
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Hình chóp tam giác đều \(S.DEF\) có:
a) Mặt bên: \(SDE\); \(SDF\); \(SEF\)
Mặt đáy: \(DEF\)
b) Các cạnh bên bằng nhau: \(SE = SF = SD = 5\)cm
Các cạnh đáy bằng nhau: \(ED = EF = DF = 3\)cm
c) Đáy \(DEF\) là tam giác đều nên ba góc ở đáy bằng nhau và bằng \(60^\circ \)
CM
18 tháng 4 2017
Đáp án A
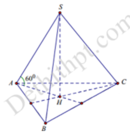
Ta có: A H = 2 3 a 2 − a 2 2 = a 3 3
S A = A H cos 60 0 = a 3 3 1 2 = 2 a 3
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Đỉnh: \(M\)
Mặt đáy: \(ABC\)
Các mặt bên: \(MAB\); \(MAC\); \(MBC\)
b) Các cạnh bên bằng nhau: \(MA = MC = 17\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 13\)cm
c) Đoạn thẳng \(MO\) là đường cao của hình chóp tam giác đều \(M.ABC\)
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Mặt đáy: \(ABCD\)
Các mặt bên: \(IAD\); \(IAB\); \(IBC\); \(ICD\)
b) Các cạnh bên bằng nhau: \(IB = IC = 18\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 14\)cm
c) Đoạn thẳng \(IH\) là đường cao của hình chóp
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Hình chóp tứ giác đều \(S.MNPQ\) có:
a) Mặt bên: \(SMN\); \(SNP\); \(SPQ\); \(SMQ\)
Mặt đáy: \(MNPQ\)
b) Các cạnh bên bằng nhau: \(SM = SN = SP = SQ = 15\)cm
Các cạnh đáy bằng nhau: \(MN = NP = PQ = MQ = 8\)cm
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
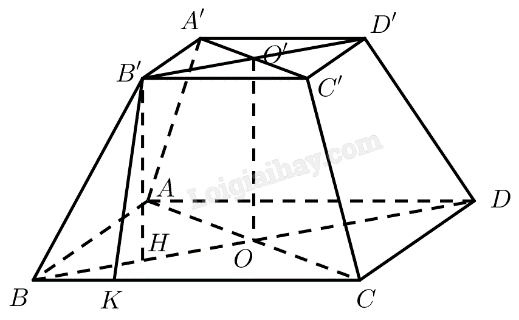
Gọi \(O\) và \(O'\) lần lượt là tâm của hai đáy.
Kẻ \(B'H \bot B{\rm{D}}\left( {H \in B{\rm{D}}} \right),B'K \bot BC\left( {K \in BC} \right)\)
\(\begin{array}{l}B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = 2a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = a\sqrt 2 \\B'D' = \sqrt {A'B{'^2} + A'{\rm{D}}{{\rm{'}}^2}} = a\sqrt 2 \Rightarrow B'O' = \frac{1}{2}B'{\rm{D'}} = \frac{{a\sqrt 2 }}{2}\end{array}\)
\(OO'B'H\) là hình chữ nhật \( \Rightarrow OH = B'O' = \frac{{a\sqrt 2 }}{2},B'H = OO' = a\)
\( \Rightarrow BH = BO - OH = \frac{{a\sqrt 2 }}{2}\)
Tam giác \(BB'H\) vuông tại \(H\) có: \(BB' = \sqrt {B'{H^2} + B{H^2}} = \frac{{a\sqrt 6 }}{2}\)
\(BCC'B'\) là hình thang cân \( \Rightarrow BK = \frac{{BC - B'C'}}{2} = \frac{a}{2}\)
Tam giác \(BB'K\) vuông tại \(K\) có: \(B'K = \sqrt {BB{'^2} - B{K^2}} = \frac{{a\sqrt 5 }}{2}\)
Các mặt bên là MAB, MAC, MBC
Các cạnh bên là MA = MB = MC = 15cm
Đường cao là MO
Các cạnh đáy là AB = AC = BC =10cm
Mặt bên: ΔAMB; ΔBMC; ΔAMC
Mặt đáy: ΔABC
Độ dài cạnh bên: 15cm
Độ dài cạnh đáy: 10cm