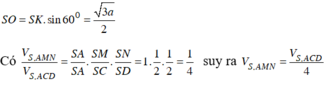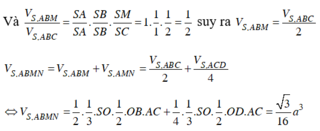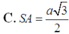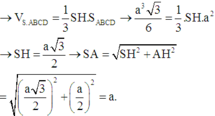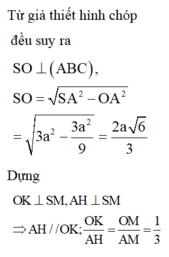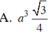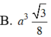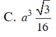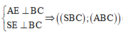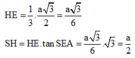Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

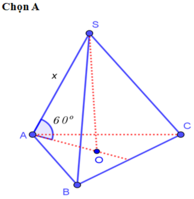
Gọi O là tâm đáy, M là trung điểm AB
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABC\right)\\OM\perp AB\end{matrix}\right.\) \(\Rightarrow\widehat{SMO}\) hay là góc giữa mặt bên và mặt đáy
\(\Rightarrow\widehat{SMO}=60^0\) \(\Rightarrow SO=OM.tan60^0=\dfrac{1}{3}CM.tan60^0=\dfrac{1}{3}AB.\dfrac{\sqrt{3}}{2}.tan60^0=\dfrac{a}{2}\)
\(CO=\dfrac{2}{3}CM=\dfrac{2}{3}.AB\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SC=\sqrt{SO^2+OC^2}=\dfrac{a\sqrt{21}}{6}\)

Lời giải:
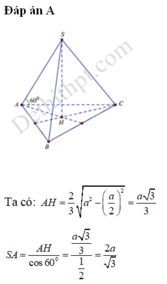
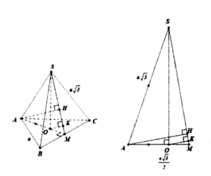
$H$ là chân đường cao của hình chóp đều nên $H$ chính là tâm đường tròn ngoại tiếp tam giác $ABC$
Kẻ $HM\perp BC$. Dễ thấy $M$ là trung điểm $BC$ và $SBC$ cân tại $S$ nên $SM\perp BC$
Do đó:
$\angle ((SBC), (ABC))=\angle (SM, HM)$
$=\widehat{SMH}=60^0$
$\frac{SH}{HM}=\tan \widehat{SMH}=\tan 60^0=\sqrt{3}$
$\Rightarrow SH=\sqrt{3}HM$
Mà: $HM=\frac{1}{3}AM=\frac{1}{3}.\sqrt{AB^2-BM^2}=\frac{1}{3}\sqrt{AB^2-(\frac{BC}{2})^2}=\frac{\sqrt{3}}{6}a$
Do đó: $SH=\sqrt{3}HM=\frac{3}{6}a=\frac{1}{2}a$

Chọn đáp án C
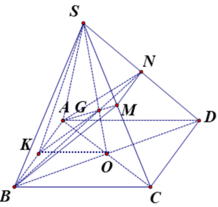
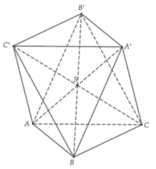
Do S. ABCD đều, có trọng tâm G của tam giác SAC cũng là trọng tâm của SBD.
Nên M, N lần lượt là trung điểm của SC, SD.
Do đó
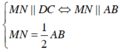
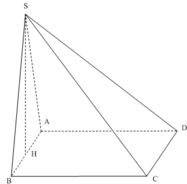
Gọi K là trung điểm của AB, O = AC ∩ BD do S. ABCD đều nên SO ⊥ (ABCD)
ABCD là hình vuông nên có SKO = 60 0
Xét tam giác SKO vuông tại O có KO = a 2 và SKO = 60 0 suy ra: