Cho HCN ABCD. Gọi M là 1 điểm nằm trong HCN biết MA = 30cm, MD = 40cm,MB = 50cm. Tính MC???Cho tam giác ABC vuông tại A(AB>AC). Lấy AB,BC làm cạnh dựng các hình vuông ABDE,BCFG vào phía trong của tam...

Gọi giao điểm của hai đường chéo là O giao điểm của hai cạnh bên là S,giao điểm của SO với AB,CD lần lượt là X,Y.
Ta có AX//YC nên theo định lý Ta lét ta có:
$\frac{AX}{YC}$=$\frac{AO}{OC}$=$\frac{AB}{DC}$=$\frac{AX}{DY}$
=>YC=DY
Vậy Y là trung điểm của DC.
Ta có AB//DC theo định lý Ta-lét ta có:
$\frac{AX}{DY}$=$\frac{SX}{XY}$=$\frac{XB}{YC}$
mà DY=YC(c/m trên)
=>AX=XB=>X là trung điểm của AB
Vậy giao điểm của SO với AB,CD tại trung điểm của các cạnh đó
=>đpcm
Ta cũng dễ dàng chứng mình được đường thẳng chứa 4 điểm đó là trùng trực của hai cạnh đấy sao khi chừng minh chúng thẳng hàng ở trên nhé!

Đúng(0)

C

caikeo

27 tháng 12 2017

Gọi giao điểm của hai đường chéo là O giao điểm của hai cạnh bên là S,giao điểm của SO với AB,CD lần lượt là X,Y.
Ta có AX//YC nên theo định lý Ta lét ta có:
AXYC=AOOC=ABDC=AXDY
=>YC=DY
Vậy Y là trung điểm của DC.
Ta có AB//DC theo định lý Ta-lét ta có:
AXDY=SXXY=XBYC
mà DY=YC(c/m trên)
=>AX=XB=>X là trung điểm của AB
Vậy giao điểm của SO với AB,CD tại trung điểm của các cạnh đó
=>đpcm

Đúng(0)

VH

Văn Hoàng Huy

8 tháng 6 2016 - olm

Năn nỉ các bạn nào giỏi toán giải giùm em, em đang cần gấp ạ!!!!!!BÀI 1:Chứng minh rằng nếu hai cạnh bên của một hình thang cắt nhau thì đường thẳng đi qua giao điểm đó và giao điểm 2 đường chéo sẽ đi qua trung điểm các đáy của hình thang.BÀI 2:Tam giác ABC có BC= 2AB và góc ABC=120 độ. Chứng minh rằng đường trung tuyến BM vuông góc ABBÀI 3:Cho tam giác ABC vuông tại A. về phía ngoài tam giác...

Đọc tiếp

#Toán lớp 8

0

LM

Lê Minh Thuận

13 tháng 1

Cho tam giác ABC vuông tại A . Có cạnh AB = 30cm , AC = 40cm , BC = 50cm . Lấy điểm D trên cạnh AB , điểm E trên cạnh AC sao cho tứ giác DECB hình thang có chiều cao là 12cm . Tính diện tích hình thang DECB

#Toán lớp 6

2

AH

Akai Haruma

Giáo viên

4 tháng 2

Lời giải:

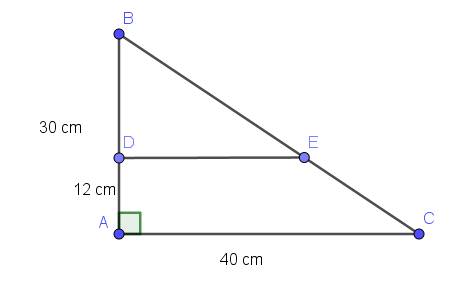
$BD=AB-DA=30-12=18$ (cm)

Diện tích tam giác ABC:

$AB.AC:2=30.40:2=600$ (cm²)

Diện tích tam giác ABC cũng bằng;

$S_{BDE}+S_{ADEC}=BD.DE:2+(DE+AC).AD:2$
$=18.DE:2+(DE+40).12:2$

$=9DE+6(DE+40)$ (cm²)

Vậy: $600=9DE+6(DE+40)=15DE+240$

$\Rightarrow DE=(600-240):15=24$ (cm)

Diện tích hình thang DECA:

$(DE+AC).DA:2=(24+40).12:2=384$ (cm²)

Đúng(1)

AH

Akai Haruma

Giáo viên

4 tháng 2

Hình vẽ:

Đúng(0)

TH

Trần Hoài Anh

28 tháng 2 2022

Cho tam giác ABC gọi M là trung điểm của cạnh BC trên tia đối của tia MA lấy điểm D sao cho MD = MA A CM AB=CD AC VUÔNG GÓC DC B CM MA=MB=MC C KẺ AH VUÔNG GÓC BC TẠI H CM AH<=BC/2

#Toán lớp 7

0

NL

Nguyễn Lê Trình

8 tháng 10 2017 - olm

Bài 1) cho hình chữ nhật ABCD và 1 điểm M nằm bên trong hình chữ nhật

chứng minh: MA^2+MC^ =MB^2+MD^2

Bài 2) cho hình tam giác ABC vuông tại A(AB<AC). Vẽ AH vuông góc BC tại H; d là điểm rên cạnh AC sao cho AD=AB

Vẽ DE vuông góc BC tại E.

chứng minh: HA=HE

#Toán lớp 7

0

NN

nguyễn như bảo hân

8 tháng 12 2019 - olm

Cho tam giác ABC vuông tại A. M là trung điểm của các cạnh Bc. Kẻ MD vuông góc vs AB, ME vuông góc vs AC.

a. CM tứ giác ADME là hcn

b. CM DECB là hình thang

c. Tam giác ABC cân có thêm điều kiện gì để DECB là hình thang cân

d. Cho AB= 6, AC= 8. Tím AM? Tính diện tích ABC và diện tích hcn ABCD

#Toán lớp 8

0

NH

Nguyễn Hữu Việt

24 tháng 3 2015 - olm

Cho hình tam giác ABC là tam giác vuông ở A , cạnh AB bằng 30cm, cạnh AC bằng 40cm, cạnh BC bằng 50cm. Trên AB lấy điểm D, trên AC lấy điểm E, sao cho BDEC là hình thang có hiểu cao bằng 6cm.
a) Tính độ dài 3 đường cao của tam giác ABC ?
b) Tính diện tích hình tam giác ADE ?

#Toán lớp 5

5

B

BIGBANGand2NE1

1 tháng 3 2016

đúng bài mình cần nè

Đúng(0)

ND

Nguyễn Đăng Khang

26 tháng 3 2016

mình cũng đang cần bài đó

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP