Question

[Buddy]

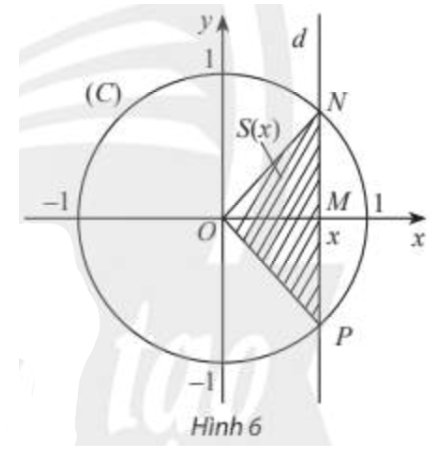
Trong mặt phẳng toạ độ \(Oxy\), cho đường tròn \(\left( C \right)\) tâm \(O\), bán kính bằng 1. Một đường thẳng \(d\) thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm \(M\) có hoành độ \(x\left( { - 1 < x < 1} \right)\) và cắt đường tròn \(\left( C \right)\) tại các điểm \(N\) và \(P\) (xem Hình 6).

a) Viết biểu thức \(S\left( x \right)\) biểu thị diện tích của tam giác \(ONP\).

b) Hàm số \(y = S\left( x \right)\) có liên tục trên \(\left( { - 1;1} \right)\) không? Giải thích.

c) Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right)\) và \(\mathop {\lim }\limits_{x \to  - {1^ + }} S\left( x \right)\).

Answer 1

[Hà Quang Minh]

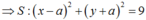
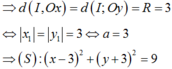
a) Ta có: \(\left( C \right):{x^2} + {y^2} = 1 \Leftrightarrow y =  \pm \sqrt {1 - {x^2}} \).

Độ dài \(OM\) chính là giá trị tuyệt đối của hoành độ của điểm \(M\). Vậy \(OM = \left| x \right|\).

Độ dài \(MN\) chính là giá trị tuyệt đối của tung độ của điểm \(N\). Vậy \(MN = \left| {\sqrt {1 - {x^2}} } \right| = \sqrt {1 - {x^2}} \).

\(S\left( x \right) = {S_{ONP}} = \frac{1}{2}.NP.OM = MN.OM = \sqrt {1 - {x^2}} .\left| x \right|\).

b) Xét hàm số  \(S\left( x \right) = \sqrt {1 - {x^2}} .\left| x \right| = \left\{ {\begin{array}{*{20}{c}}{x\sqrt {1 - {x^2}} }&{khi\,\,0 \le x \le 1}\\{ - x\sqrt {1 - {x^2}} }&{khi\,\, - 1 \le x < 0}\end{array}} \right.\).

ĐKXĐ: \(1 - {x^2} \ge 0 \Leftrightarrow  - 1 \le x \le 1\)

Hàm số \(S\left( x \right)\) có tập xác định là \(\left[ { - 1;1} \right]\).

Vậy hàm số \(S\left( x \right)\) xác định trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\) nên liên tục trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).

Ta có: \(S\left( 0 \right) = 0.\sqrt {1 - {0^2}}  = 0\)

\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {x\sqrt {1 - {x^2}} } \right) = 0.\sqrt {1 - {0^2}}  = 0\)

\(\mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x\sqrt {1 - {x^2}} } \right) =  - 0.\sqrt {1 - {0^2}}  = 0\)

Vì \(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = 0\) nên \(\mathop {\lim }\limits_{x \to 0} S\left( x \right) = 0 = S\left( 0 \right)\)

Vậy hàm số \(S\left( x \right)\) liên tục tại điểm \({x_0} = 0\). Vậy hàm số \(S\left( x \right)\) liên tục trên \(\left( { - 1;1} \right)\).

c) \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x\sqrt {1 - {x^2}} } \right) = 1.\sqrt {1 - {1^2}}  = 0\)

\(\mathop {\lim }\limits_{x \to  - {1^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to  - {1^ + }} \left( { - x\sqrt {1 - {x^2}} } \right) =  - 1.\sqrt {1 - {{\left( { - 1} \right)}^2}}  = 0\)