Giả sử ABC là tam giác vuông cân tại A với độ dài cạnh góc vuông bằng 1. Ta tạo ra các hình vuông theo các bước sau đây :
- Bước 1 : Dựng hình vuông mầu xám có một đỉnh là A, ba đỉnh còn lại là các trung điểm của ba cạnh AB, BC và AC (H1). Kí hiệu hình vuông này là (1)
- Bước 2 : Với 2 tam giác vuông cân mầu trắng còn lại như trong hình 1, ta lại tạo được 2 hình vuông mầu xác khác theo...
Đọc tiếp
Giả sử ABC là tam giác vuông cân tại A với độ dài cạnh góc vuông bằng 1. Ta tạo ra các hình vuông theo các bước sau đây :
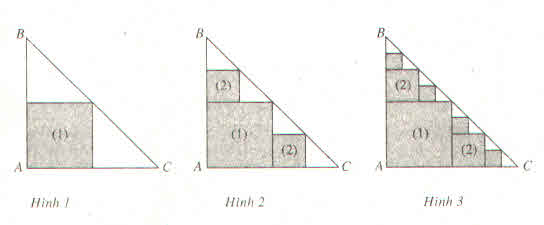
- Bước 1 : Dựng hình vuông mầu xám có một đỉnh là A, ba đỉnh còn lại là các trung điểm của ba cạnh AB, BC và AC (H1). Kí hiệu hình vuông này là (1)
- Bước 2 : Với 2 tam giác vuông cân mầu trắng còn lại như trong hình 1, ta lại tạo được 2 hình vuông mầu xác khác theo cách trên, kí hiệu là (2) (H2)
- Bước 3 : Với 4 tam giác vuông cân mầu trắng như trong hình 2, ta lại tạo được 4 hình vuông với mầu xám theo cách trên (H3)
- ..........
- Bước n : Ở bước này ta có \(2^{n-1}\) hình vuông với mầu sám được tạo thành theo cách trên, kí hiệu là (n)
a) Gọi \(u_n\) là tổng diện tích của tất cả các hình vuông mới được tạo thành ở bước thứ n.
Chứng minh rằng :
\(u_n=\dfrac{1}{2^{n+1}}\)
b) Gọi \(S_n\) là tổng diện tích của tất cả các hình vuông mầu xám có được sau n bước. Quan sát hình vẽ để dự đoán giới hạn của \(S_n\) khi \(n\rightarrow+\infty\). Chứng minh dự đoán đó ?
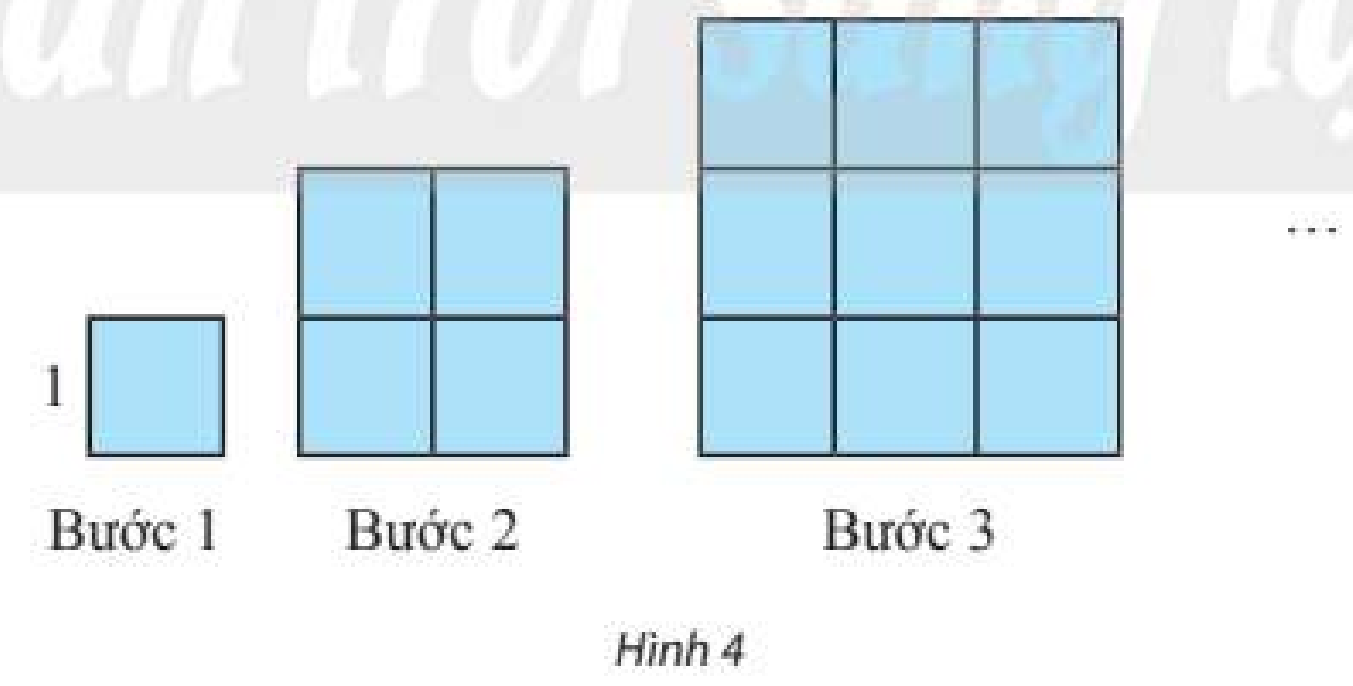



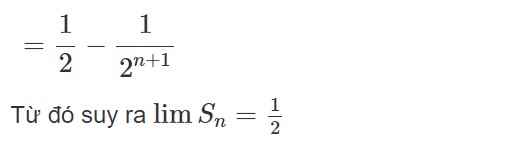



a) Ta có: \({u_1} = {1^2};{u_2} = {2^2};{u_3} = {3^2};...;{u_n} = {n^2}\)
\(\begin{array}{l}{u_n} > 10000 \Leftrightarrow {n^2} > 10000 = {100^2} \Leftrightarrow n > 100\\{u_n} > 1000000 \Leftrightarrow {n^2} > 1000000 = {1000^2} \Leftrightarrow n > 1000\end{array}\)
b) \({u_n} > S \Leftrightarrow {n^2} > S \Leftrightarrow n > \sqrt S \).
Vậy với các số tự nhiên \(n > \sqrt S \) thì \({u_n} > S\).