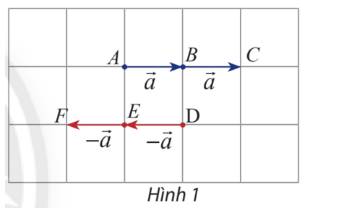
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) sau đây:

\(\overrightarrow {OM} .\overrightarrow {ON} = \left| {\overrightarrow {OM} } \right|.\left| {\overrightarrow {ON} } \right|.cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right)\)\( = cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right) = cos\left( {\alpha - \beta } \right)\)
\(\overrightarrow {OM} .\overrightarrow {ON} = {x_M}.{x_N} + {y_M}.{y_N}\)
Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.

\(cos\left(\alpha-\beta\right)=x_M\cdot x_N=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\\ cos\left(\alpha+\beta\right)=cos\left[\alpha-\left(-\beta\right)\right]=cos\alpha\cdot cos\left(-\beta\right)+sin\alpha\cdot sin\left(-\beta\right)=cos\alpha\cdot cos\beta-sin\alpha\cdot sin\beta\)