Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M thuộc d, quỹ tích những điểm N thỏa mãn \(2\overrightarrow{OM}+\overrightarrow{ON}=\overrightarrow{0}\) là ảnh của d qua phép vị tự tâm O tỉ số \(k=-2\)
\(\Rightarrow\) Quỹ tích N là đường thẳng d' có pt \(x+y-6=0\)
d' không cắt (C) nên không tồn tại cặp điểm M, N nào thỏa mãn yêu cầu

1/ \(\overrightarrow{AB}^2-\overrightarrow{AD}^2=\overrightarrow{BC}^2-\overrightarrow{CD}^2\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{AB}-\overrightarrow{AD}\right)=\left(\overrightarrow{BC}+\overrightarrow{CD}\right)\left(\overrightarrow{BC}-\overrightarrow{CD}\right)\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right).\overrightarrow{DB}=\overrightarrow{BD}\left(\overrightarrow{BC}-\overrightarrow{CD}\right)=\overrightarrow{DB}\left(\overrightarrow{CB}+\overrightarrow{CD}\right)\)
Gọi M là trung điểm BD
\(\Rightarrow2\overrightarrow{AM}.\overrightarrow{DB}=2\overrightarrow{CM}.\overrightarrow{DB}\)
\(\Leftrightarrow\overrightarrow{DB}.\left(\overrightarrow{AM}-\overrightarrow{CM}\right)=0\)
\(\Leftrightarrow\overrightarrow{BD}.\overrightarrow{AC}=0\)
2/ \(A=\left|\overrightarrow{a}-\overrightarrow{b}\right|\Rightarrow A^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\)
\(=a^2+b^2-2ab.cos\left(\overrightarrow{a};\overrightarrow{b}\right)=4^2+5^2-2.4.5.cos120^0=61\)
\(\Rightarrow A=\sqrt{61}\)
b/ \(B=\left|2\overrightarrow{a}+\overrightarrow{b}\right|\Rightarrow B^2=4a^2+b^2+4\overrightarrow{a}.\overrightarrow{b}\)
\(=4a^2+b^2+4ab.cos120^0=49\)
\(\Rightarrow B=7\)
3/ \(\left|\overrightarrow{x}\right|=\left|\overrightarrow{a}-2\overrightarrow{b}\right|\Rightarrow\left|\overrightarrow{x}\right|^2=a^2+4b^2-4\overrightarrow{a}.\overrightarrow{b}=12\)
\(\Rightarrow\left|\overrightarrow{x}\right|=2\sqrt{3}\)
\(\left|\overrightarrow{y}\right|^2=a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=5\Rightarrow\left|\overrightarrow{y}\right|=\sqrt{5}\)
\(\overrightarrow{x}.\overrightarrow{y}=\left(\overrightarrow{a}-2\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=a^2+2b^2-3\overrightarrow{a}.\overrightarrow{b}=4\)
\(\Rightarrow cos\alpha=\frac{\overrightarrow{x}.\overrightarrow{y}}{\left|\overrightarrow{x}\right|.\left|\overrightarrow{y}\right|}=\frac{4}{2\sqrt{15}}=\frac{2\sqrt{15}}{15}\)

1.
\(cos\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)=\dfrac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\dfrac{10}{10.\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(\Rightarrow\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)=45^0\)
2.
a.
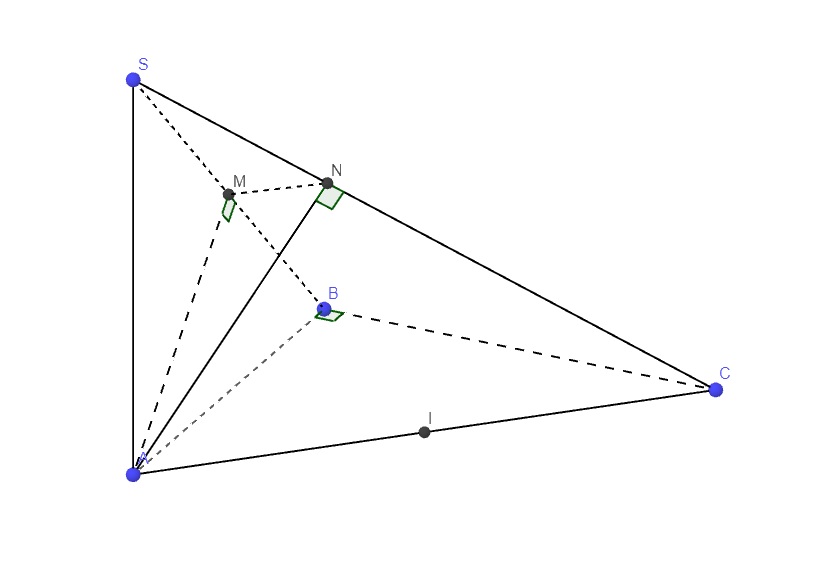
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\) (1)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=1\Rightarrow\widehat{SBA}=45^0\)
b.
Từ (1) \(\Rightarrow BC\perp AM\)
Mà \(AM\perp SB\left(gt\right)\) \(\Rightarrow AM\perp\left(SBC\right)\) (2)
\(\Rightarrow AM\perp MN\Rightarrow\Delta AMN\) vuông tại M
Từ (2) \(\Rightarrow AM\perp SC\), mà \(SC\perp AN\left(gt\right)\)
\(\Rightarrow SC\perp\left(AMN\right)\) (3)
Lại có \(SA\perp\left(ABC\right)\) theo giả thiết
\(\Rightarrow\) Góc giữa (AMN) và (ABC) bằng góc giữa SA và SC hay là góc \(\widehat{ASC}\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{ASC}=\dfrac{AC}{SA}=\sqrt{2}\Rightarrow\widehat{ASC}\approx54^044'\)
Từ (3) \(\Rightarrow AN\) là hình chiếu vuông góc của AC lên (AMN)
\(\Rightarrow\widehat{CAN}\) là góc giữa AC và (AMN)
Mà \(\widehat{CAN}=\widehat{ASC}\) (cùng phụ \(\widehat{ACS}\)) \(\Rightarrow\widehat{CAN}=...\)
c.
\(\left\{{}\begin{matrix}IC=\dfrac{1}{2}AC\left(gt\right)\\AI\cap\left(SBC\right)=C\end{matrix}\right.\) \(\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}d\left(A;\left(SBC\right)\right)\)
Mà từ (2) ta có \(AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(SA=AB\left(gt\right)\Rightarrow\Delta SAB\) vuông cân tại A
\(\Rightarrow AM=\dfrac{1}{2}SB=\dfrac{a\sqrt{2}}{2}\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}AM=\dfrac{a\sqrt{2}}{4}\)

Đáp án B và D giống nhau nên chắc chắn cả 2 đều đúng
Kiểm tra 2 đáp án A và C:
\(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{MC}+\overrightarrow{MD}\right)=\frac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{MB}+\overrightarrow{BD}\right)=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{BD}\right)\)
Vậy đáp án A đúng nên đáp án C sai

Gọi D là trung điểm BC và G là trọng tâm tam giác ABC
Theo tính chất trọng tâm: \(AG=\dfrac{2}{3}AD\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=\left|\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MA}+\overrightarrow{CM}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|\overrightarrow{BA}+\overrightarrow{CA}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}\right|=\left|-2\overrightarrow{AD}\right|\)
\(\Leftrightarrow MG=\dfrac{2}{3}AD=AG\)
\(\Rightarrow\) Tập hợp M là mặt cầu tâm G bán kính AG với G là trọng tâm tam giác ABC

\(cos\left(\alpha-\beta\right)=x_M\cdot x_N=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\\ cos\left(\alpha+\beta\right)=cos\left[\alpha-\left(-\beta\right)\right]=cos\alpha\cdot cos\left(-\beta\right)+sin\alpha\cdot sin\left(-\beta\right)=cos\alpha\cdot cos\beta-sin\alpha\cdot sin\beta\)