Cho ∆ABC vuông tại A, phân giác AD, \(\dfrac{BD}{BC}=\dfrac{3}{7}\), BC = 20. Tính AB,...
Đọc tiếp
Cho ∆ABC vuông tại A, phân giác AD, \(\dfrac{BD}{BC}=\dfrac{3}{7}\), BC = 20. Tính AB, AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 8 2021
Bài 2:
Ta có: \(\dfrac{BD}{DC}=\dfrac{3}{7}\)
nên \(\dfrac{AB}{AC}=\dfrac{3}{7}\)
hay \(AB=\dfrac{3}{7}AC\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{49}+AC^2=20^2=400\)
\(\Leftrightarrow AC^2=\dfrac{9800}{29}\)
\(\Leftrightarrow AC=\dfrac{70\sqrt{58}}{29}\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{7}\cdot AC=\dfrac{30\sqrt{58}}{29}\left(cm\right)\)
6 tháng 8 2019
Câu hỏi của Trần Dần - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo nhé!
30 tháng 10 2021
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔBCD vuông tại B có BA là đường cao
nên \(AD\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=AD\cdot AC\)
TD
Cho tam giác ABC vuông tại A, phân giác AD, \(\frac{BD}{BC}\)= \(\frac{3}{7}\), BC = 20. Tính AB, AC
1
6 tháng 8 2019
Theo bài ra ta có:
\(\frac{BD}{BC}=\frac{3}{7}\Rightarrow\frac{BD}{CD}=\frac{3}{4}\)
Tam giác ABC có phân giác AD
=> \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{3}{4}\)=> Đặt \(AB=3a\)=> \(AC=4a\)
Tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2\)
<=> \(\left(3a\right)^2+\left(4a\right)^2=20^2\)
<=> \(9a^2+16a^2=400\)
<=> \(a^2=16\Leftrightarrow a=4\)
=> AB=12; AC =16
NA
1
CL
20 tháng 6 2023
Để tính AB và AC, ta sẽ sử dụng định lý Pythagoras trong tam giác vuông.
Với ∆ABC vuông tại A và BD là phân giác của góc B, ta có:
BD/BC = 3/4
Vì BD/BC = 3/4, ta có thể xác định giá trị của BD và CD:
BD = (3/4) * BC = (3/4) * 20cm = 15cm CD = BC - BD = 20cm - 15cm = 5cm
Với AB > AC, ta có thể gọi AB = x và AC = y (với x > y).
Áp dụng định lý Pythagoras trong tam giác vuông ABC, ta có:
AB^2 = AC^2 + BC^2
x^2 = y^2 + 20^2
Ta cũng biết rằng BD là phân giác của góc B, do đó:
AD = DC = 5cm
Áp dụng định lý Pythagoras trong tam giác vuông ABD, ta có:
AB^2 = AD^2 + BD^2
x^2 = 5^2 + 15^2
x^2 = 25 + 225
x^2 = 250
Từ phương trình trên, ta có x = √250 = 5√10
Do đó, AB = 5√10 cm.
Tiếp theo, ta sẽ tính giá trị của y (AC).
Áp dụng định lý Pythagoras trong tam giác vuông ACD, ta có:
AC^2 = AD^2 + CD^2
y^2 = 5^2 + 5^2
y^2 = 25 + 25
y^2 = 50
Từ phương trình trên, ta có y = √50 = 5√2
Do đó, AC = 5√2 cm.
Tóm lại, AB = 5√10 cm và AC = 5√2 cm.
23 tháng 6 2021
Kẻ \(AH\perp BC\) tại H
Áp dụng hệ thức lượng trong tam giác vuông BAC có:
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
Do AD và AE lần lượt là hai tia phân giác trong và ngoài tại đỉnh A
\(\Rightarrow AD\perp AE\)
Áp dụng hệ thức lượng vào tam giác vuông AED có:
\(\dfrac{1}{AE^2}+\dfrac{1}{AD^2}=\dfrac{1}{AH^2}\) (AH là đường cao của tam giác AED do \(AH\perp BC\) hay \(AH\perp ED\))
\(\Rightarrow\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AE^2}+\dfrac{1}{DA^2}\)
Vậy...
TT
22 tháng 1 2021
CMR : tan\(\dfrac{B}{2}=\dfrac{AC}{BC+AB}\) nhé mình ghi thiếu
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2021
Theo tính chất phân giác:
\(\dfrac{AD}{AB}=\dfrac{CD}{BC}=\dfrac{AD+CD}{AB+BC}=\dfrac{AC}{AB+BC}\)
\(\Rightarrow tan\dfrac{B}{2}=\dfrac{AD}{AB}=\dfrac{AC}{AB+BC}\) (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
Từ hình vẽ thì hướng giải như sau:
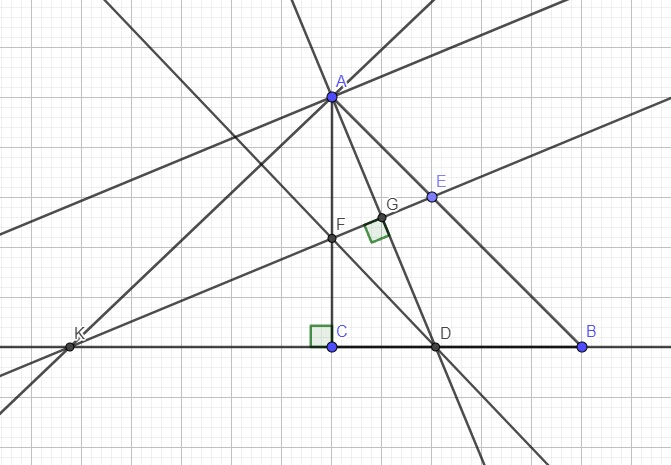
Dễ dàng nhận ra \(DF\perp AK\), từ đó biết vtpt của DF \(\Rightarrow\) phương trình DF
\(\Rightarrow\) Tọa độ F (là giao của DF và đường tròn tâm D bán kính DE do DE=DF)
Biết tọa độ F \(\Rightarrow\) viết được pt AD qua D vuông góc EF
\(\Rightarrow\) Tọa độ A từ là giao AK và AD
\(\Rightarrow\) Phương trình AB qua A và E, phương trình AC qua A và F, phương trình BC qua D và vuông góc AF
BD/BC=3/7
=>BD/CD=3/4
=>AB/AC=3/4
=>AB/3=AC/4=k
=>AB=3k; AC=4k
AB^2+AC^2=BC^2
=>25k^2=400
=>k=4
=>AB=12cm; AC=16cm