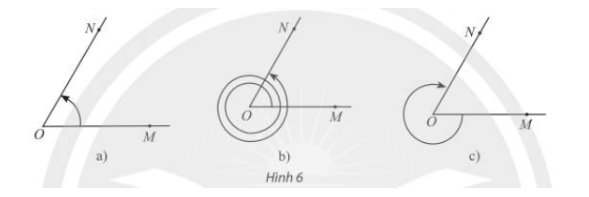
Cho \(\widehat {MON} = {60^ \circ }\). Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM,ON).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left(OA,OM\right)=120^o+k\cdot360^o,k\in Z\\ \left(OA,ON\right)=-75^o+k\cdot360^o,k\in Z\)

Công thức tổng quát số đo của góc lượng giác \(\left(Ox,ON\right)=70^o+k\cdot360,k\in Z\)
Công thức tổng quát số đo của lượng giác
\(\left(Ox,OP\right)=\left(Ox,OM\right)+\left(OM,OP\right)=-50-120^o+m\cdot360^o=-170^o+m\cdot360^o,m\in Z\)

a) Ta có:
- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là
sđ\((Ou,Ov) = {30^ \circ } + n{.360^ \circ }\)
- Các góc lượng giác tia đầu Ov, tia cuối Ow có số đo là
sđ \((Ov,Ow) = {45^ \circ } + m{.360^ \circ }\)
- Các góc lượng giác tia đầu Ou, tia cuối Ow có số đo là
sđ \((Ou,Ow) = {75^ \circ } + k{.360^ \circ }\)
b) Với các góc lượng giác ở câu a, ta có:
\(sđ(Ou,Ov) +sđ (Ov,Ow)\)
\( = {30^ \circ } + n{.360^ \circ } + {45^ \circ } + m{.360^ \circ } \)
\(= {75^ \circ } + (n+m){.360^ \circ } \)
\(= {75^ \circ } + k{.360^ \circ = sđ (Ou,Ow)} \)
với k = n + m

Vì mâm bánh xe ô tô được chia thành năm phần bằng nhau nên mỗi phần có số đo bằng \(\dfrac{360^o}{5}=72^o\)
Ta có: \(\left(ON,OM\right)=\left(ON,Ox\right)+\left(Ox,OM\right)\\ \Rightarrow\left(ON,Ox\right)=99^o\)
Công thức số đo tổng quát của góc lượng giác \(\left(ON,Ox\right)=99^o+k\cdot360^o,k\in Z\)

Tham khảo:
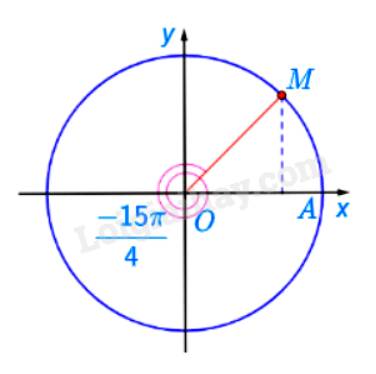
Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.
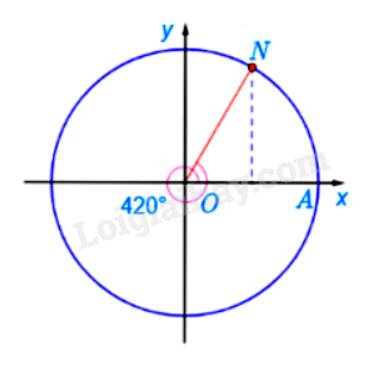
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)

Điểm biểu diễn góc lượng giác x có \(cosx = \frac{{ - 1}}{2}\) là M và N.
Số đo góc lượng giác có điểm biểu diễn M là: \(\frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
Số đo góc lượng giác có điểm biểu diễn N là: \(\frac{{4\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).

a) Các tia Om, On tương ứng là tia phân giác của góc yOz và xOz vì:
Tia Om nằm trong góc yOz và \(\widehat {yOm} = \widehat {mOz}\)
Tia On nằm trong góc xOz và \(\widehat {xOn} = \widehat {nOz}\)
b) Vì các tia Om, On tương ứng là tia phân giác của góc yOz và xOz nên: \(\widehat {yOm} = \widehat {mOz} = \frac{1}{2}.\widehat {yOz};\widehat {xOn} = \widehat {nOz} = \frac{1}{2}.\widehat {xOz}\)
Mà tia Oz nằm trong góc xOy nên \(\widehat {yOz} + \widehat {xOz} = \widehat {xOy}\)
\( \Rightarrow \widehat {mOz} + \widehat {zOn} = \frac{1}{2}.\widehat {yOz} + \frac{1}{2}.\widehat {xOz} = \frac{1}{2}.\widehat {xOy}\)
Mà tia Oz nằm trong góc mOn nên \(\widehat {mOz} + \widehat {zOn} = \widehat {mOn}\) và \(\widehat {xOy} = 90^\circ \)
\( \Rightarrow \widehat {mOn} = \frac{1}{2}.90^\circ = 45^\circ \)

Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
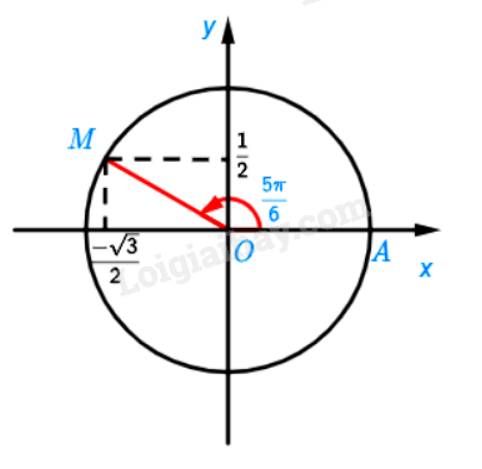
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)

a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)
b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)
a, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o\)
b, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o+2\cdot360^o=780^o\)
c, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(\dfrac{5}{6}\cdot\left(-360^o\right)=-300^o\)
Công thức tổng quát của số đo góc lượng giác (OM, ON) \(=60^o+360^o\cdot k,k\in Z\)