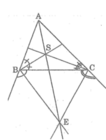
Cho tam giác ABC có các đường phân giác trong là BE và CF cắt nhau tại M và các đường phân giác ngoài của các góc B và góc C cắt nhau tại N. Chứng minh tứ giác BMNC là tứ giác nội tiếp
Vẽ hình ra luôn
Giúp mình vs lớp 9 ơi !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 5 2017
Tự Vẽ Hình Nhé :
Theo tính chất đường phân giác ngoài của một góc luôn vuông góc với đường phân giác ngoài của góc đó
=> \(\widehat{MBN}=\widehat{MCN}=90^0\)nên hai góc \(\widehat{MBN}\)và \(\widehat{MCN}\)cùng nhìn MN dưới một góc bằng 90 độ. vậy Tứ giác MBNC nội tiếp đường tròn đường kính MN
W
28 tháng 5 2017
mk ko có bít làm sao jờ ?
?????????????????
Cho tam giác ABC có các đường phân giác trong là BE và CF cắt nhau tại M và các đường phân giác ngoài của các góc B và góc C cắt nhau tại N. Chứng minh tứ giác BMNC là tứ giác nội tiếp
Vẽ hình ra luôn
- mk ko bít
- ????
- tự làm nhé ^_^ !
9 tháng 9 2021
a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}\)
nên BCEF là tứ giác nội tiếp
Xét tứ giác CDHE có
\(\widehat{HDC}+\widehat{HEC}=180^0\)
Do đó: CDHE là tứ giác nội tiếp
CM
5 tháng 6 2017
Ta có: BS ⊥ BE (tính chất đường phân giác của hai góc kề bù)
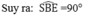
Và CS ⊥ CE (tính chất đường phân giác của hai góc kề bù)
Xét tứ giác BSCE ta có:
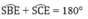
Vậy tứ giác BSCE nội tiếp đường tròn
28 tháng 7 2023
a: góc AFH+góc AEH=180 độ
=>AEHF nội tiếp
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b: BFEC nội tiếp
=>góc IBF=góc IEC
Xét ΔIBF và ΔIEC có
góc IBF=góc IEC
góc I chung
=>ΔIBF đồng dạng với ΔIEC
=>IB/IE=IF/IC
=>IB*IC=IE*IF
27 tháng 7 2023
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
góc CDH+góc CEH=90+90=180 độ
=>CDHE nội tiếp
b: góc AFH+góc AEH=180 độ
=>AFHE nội tiếp
góc FEH=góc BAD
góc DEH=góc FCB
mà góc BAD=góc FCB
nên góc FEH=góc DEH
=>EH là phân giác của góc FED
Xét ΔBFE và ΔDHE có
góc BEF=góc DEH
góc BFE=góc DHE
=>ΔBFE đồng dạng với ΔDHE
21 tháng 1 2022
a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BCEF là tứ giác nội tiếp
Xét tứ giác CDHE có
\(\widehat{CDH}+\widehat{CEH}=180^0\)
Do đó: CDHE là tứ giác nội tiếp
b: \(\widehat{FEB}=\widehat{BAD}\)(vì AFHE là tứ giác nội tiếp)
\(\widehat{BED}=\widehat{FCB}\)(BFEC là tứ giác nội tiếp)
mà \(\widehat{BAD}=\widehat{FCB}\)
nên \(\widehat{FEB}=\widehat{BED}\)
hay EB là tia phân giác góc FED
Hình Vẽ Đấy
còn bài nào toán hình k