Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) BS, BE là phân giác của hai góc kề bù nên góc SBE =900
tương tự góc SCE = 900 => tứ giác BSCE nội tiếp
b) góc ASB = \(180^0-\left(gocBAS+gocABS\right)\)(tổng 3 góc trog tg ASB)
=> góc ASB = \(180^0-\left(\frac{gócABC}{2}+\frac{gocBAC}{2}\right)=180^0-\frac{gocABC+gocBAC}{2}\)
= \(180^0-\frac{180^0-gocACB}{2}=90^0+\frac{gocACB}{2}\) (1)
Ta lại có : góc BSE = 900 - góc BES mà góc BES = góc BCS( BSCE nội tiếp) ; góc BCS = góc ACB/2 => góc BES = góc ACB/2
=> góc BSE = \(90^0-\frac{gócACB}{2}\)(2)
từ (1) và (2) => góc ASB + góc BSE = 1800. Vậy A, S, E thẳng hàng

Tự Vẽ Hình Nhé :
Theo tính chất đường phân giác ngoài của một góc luôn vuông góc với đường phân giác ngoài của góc đó
=> \(\widehat{MBN}=\widehat{MCN}=90^0\)nên hai góc \(\widehat{MBN}\)và \(\widehat{MCN}\)cùng nhìn MN dưới một góc bằng 90 độ. vậy Tứ giác MBNC nội tiếp đường tròn đường kính MN
mk ko có bít làm sao jờ ?
?????????????????
Cho tam giác ABC có các đường phân giác trong là BE và CF cắt nhau tại M và các đường phân giác ngoài của các góc B và góc C cắt nhau tại N. Chứng minh tứ giác BMNC là tứ giác nội tiếp
Vẽ hình ra luôn
- mk ko bít
- ????
- tự làm nhé ^_^ !

BM,BN là phân giác của hai góc kề bù
=>góc MBN=90 độ
CM,CN là phân giác của haigóc kề bù
=>góc MCN=90 độ
Vì góc MBN+góc MCN=180 độ
nên MBNC nội tiếp

a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CED=góc CAD
góc CDE=góc CAE
mà góc CAD=góc CAE(=góc CBD)
nên góc CED=góc CDE
=>CD=CE

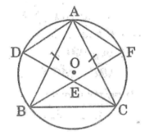

Ta có: BS ⊥ BE (tính chất đường phân giác của hai góc kề bù)
Và CS ⊥ CE (tính chất đường phân giác của hai góc kề bù)
Xét tứ giác BSCE ta có:
Vậy tứ giác BSCE nội tiếp đường tròn