giải hộ mk với mai mk pk nộp bài:
Bài 1 : thu gọn biểu thức
K
Khách
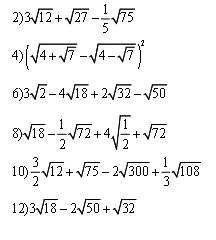
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
26 tháng 8 2021
\(1+\dfrac{1}{2}.\dfrac{3.2}{2}+\dfrac{1}{3}.\dfrac{4.3}{2}+...+\dfrac{1}{500}.\dfrac{501.500}{2}\)
\(=\dfrac{2}{2}+\dfrac{3}{2}+\dfrac{4}{2}+...+\dfrac{501}{2}\)
\(=\dfrac{2+3+4+...+501}{2}\)
\(=\dfrac{\left(501-2+1\right).\left(501+2\right)}{4}\)
\(=\dfrac{\left(501-2+1\right).\left(501+2\right)}{4}=62875\)
12 tháng 9 2021
\(a,M=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{2}{x}-\dfrac{2-x}{x\sqrt{x}+x}\right)\left(x>0;x\ne1\right)\\ M=\dfrac{x+\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{2\sqrt{x}+2-2+x}{x\left(\sqrt{x}+1\right)}\\ M=\dfrac{2x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{x\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}\\ M=\dfrac{2x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(b,M=-\dfrac{1}{2}\Leftrightarrow\dfrac{2x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=-\dfrac{1}{2}\\ \Leftrightarrow-4x=x+\sqrt{x}-2\\ \Leftrightarrow5x+\sqrt{x}-2=0\)
Đặt \(\sqrt{x}=t\)
\(\Leftrightarrow5t^2+t-2=0\\ \Delta=1^2-4\cdot5\left(-2\right)=41\\ \Leftrightarrow\left[{}\begin{matrix}t=\dfrac{-1-\sqrt{41}}{10}\\t=\dfrac{-1+\sqrt{41}}{10}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-\left(1+\sqrt{41}\right)^2}{100}=\dfrac{-42-2\sqrt{41}}{100}\\x=\dfrac{\left(\sqrt{41}-1\right)^2}{100}=\dfrac{42-2\sqrt{41}}{100}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-21-\sqrt{41}}{50}\left(L\right)\\x=\dfrac{21-\sqrt{41}}{50}\left(N\right)\end{matrix}\right.\\ \Leftrightarrow x=\dfrac{21-\sqrt{41}}{50}\)
12 tháng 9 2021
a: Ta có: \(M=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{2}{x}+\dfrac{x-2}{x\sqrt{x}+x}\right)\)
\(=\dfrac{x+\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{2\sqrt{x}+2+x-2}{x\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x}{\sqrt{x}-1}\cdot\dfrac{x}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2x\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
TN
3
C
19 tháng 10 2018
\(5-3x^2+6x=-3x^2+6x+5=-3\left(x^2-2x-5\right)\)
\(=-3\left(x^2-2x+1-6\right)\)
\(=-3\left(x^2-2x+1\right)+18\)
\(=-3\left(x-1\right)^2+18\le18\forall x\)
Dấu = xảy ra khi: \(-3\left(x-1\right)^2=0\Leftrightarrow x=1\)
Vậy : GTLN là 18 tại x = 1
T
20 tháng 10 2018
Nguyễn Hoàng Khánh Dương sai rồi nha bạn! Bạn thay x = 1 vào biểu thức xem có ra được giá trị MAX = 18 không???
Gọi biểu thức trên là A.Ta có: \(A=5-3x^2+6x=-3x^2+6x+5\)
\(=-3x^2+6x-3+8\)
\(=-3\left(x^2-2x+1\right)+8\)
\(=-3\left(x-1\right)^2+8\le8\) (do \(-3\left(x-1\right)^2\le0\forall x\))
Dấu "=" xảy ra \(\Leftrightarrow-3\left(x-1\right)^2=0\Leftrightarrow x=1\)
Vậy \(A_{max}=8\Leftrightarrow x=1\)
VD
2
11 tháng 1 2017
Đặt \(N=\left|a+1\right|-\left|a+2\right|+\left|-2\right|\)
Ta có \(N=\left|a+1\right|-\left|a+2\right|+2\)
Xét các trường hợp :
TH1. Nếu \(a\ge-1\) thì \(N=\left(a+1\right)-\left(a+2\right)+2=1\)
TH2. Nếu \(a\le-2\) thì \(N=-\left(a+1\right)-\left[-\left(a+2\right)\right]+2=3\)
TH3. Nếu \(-2< a< -1\) thì \(N=-\left(a+1\right)-\left(a+2\right)+2=-2a-1\)
Vậy : \(a\le-2\) : N = 3
-2 < a < -1 : N = -2a-1
\(a\ge-1\) : N = 1
VD
0
27 tháng 8 2021
Bài 10:
a: Thay x=3 vào A, ta được:
\(A=\left(\dfrac{1}{3+2}+\dfrac{1}{3^2-4}\right)=\dfrac{1}{5}+\dfrac{1}{5}=\dfrac{2}{5}\)
b: Ta có: P=AB
\(=\left(\dfrac{1}{x+2}+\dfrac{1}{x^2-4}\right)\cdot\dfrac{x^2+2x}{x-1}\)
\(=\dfrac{x-2+1}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{x\left(x+2\right)}{x-1}\)
\(=\dfrac{x-1}{x-2}\cdot\dfrac{x}{x-1}\)
\(=\dfrac{x}{x-2}\)
c: Để \(P=\dfrac{2}{3}\) thì \(\dfrac{x}{x-2}=\dfrac{2}{3}\)
\(\Leftrightarrow3x=2x-4\)
hay x=-4(nhận)
2: \(=6\sqrt{3}+3\sqrt{3}-\sqrt{3}=8\sqrt{3}\)
4:
\(=4+\sqrt{7}+4-\sqrt{7}-2\sqrt{16-7}=8-2\cdot3=2\)
6: \(=3\sqrt{2}-12\sqrt{2}+8\sqrt{2}-5\sqrt{2}=-6\sqrt{2}\)
8: \(=3\sqrt{2}-3\sqrt{2}+2\sqrt{2}+6\sqrt{2}=8\sqrt{2}\)
10: \(=3\sqrt{3}+5\sqrt{3}-20\sqrt{3}+2\sqrt{3}=-10\sqrt{3}\)
12: \(=9\sqrt{2}-10\sqrt{2}+4\sqrt{2}=3\sqrt{2}\)