so sánh các cạnh của tam giác ABC,biết rằng:
\(\widehat{A}=90^o\) \(\widehat{B}=45^o\) \(\widehat{C}=45^o\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
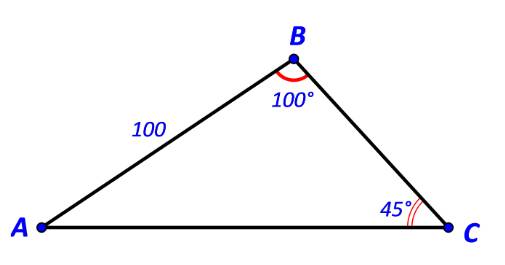
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Theo đề bài ta có AB = 4cm, BC = 7cm, AC = 6cm
Có góc đối diện với cạnh AB là góc C, góc A đối diện với cạnh BC, góc B đối diện với cạnh AC
Theo định lí về góc đối diện với cạnh lớn hơn thì lớn hơn ta có :
\( \Rightarrow \widehat A > \widehat B > \widehat C\)
b)
Vì \(\widehat{A}=\widehat{C}\) nên tam giác ABC cân tại B
\( \Rightarrow BA = BC\)
Áp dụng định lí tổng 3 góc trong tam giác ABC, có:
\( \Rightarrow \widehat B = {180^o} - {100^0} = {80^o}\)
\( \Rightarrow \widehat B > \widehat A=\widehat C\)
\( \Rightarrow AC\) là cạnh lớn nhất tam giác ABC (Quan hệ giữa góc và cạnh đối diện trong tam giác)
21 tháng 9 2023
Tham khảo:
a) Vì tam giác ABC vuông tại A nên \(\widehat{A}=90^0; \widehat{B}+\widehat{C}=90^0\)
Vì \(\widehat B > {45^o} \Rightarrow \widehat C < {45^o} \Rightarrow \widehat A > \widehat B > \widehat C \Rightarrow BC > AC > AB\)
b) Vì \(\widehat {BKC}\) là góc ngoài tại đỉnh K của tam giác ABK nên \(\widehat {BKC}>(\widehat {BAK}=90^0\)
Xét tam giác BCK, ta có :
\(\widehat {BKC} > {90^o} > \widehat {BCK}\)
\( \Rightarrow BC > BK\) ( quan hệ giữa góc và cạnh đối diện trong tam giác)
QT
1
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Ta có: \(\widehat B = {75^o},\widehat C = {45^o}\)\( \Rightarrow \widehat A = {180^o} - \left( {{{75}^o} + {{45}^o}} \right) = {60^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin {45^o}.\frac{{50}}{{\sin {{60}^o}}} \approx 40,8\)
Vậy độ dài cạnh AB là 40,8.
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.
Ta có:
\(\widehat{A}>\widehat{B}=\widehat{C}\left(90^0>45^0=45^0\right)\)
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`->`\(\text{BC > AC = AB}\).