cho nửa (o) đường kính AB, lấy C thuộc OA. Đường thẳng qua C vuông góc AB cắt (o) tại K. Gọi M là điểm bất kỳ trên cung KB. Đường CK cắt AM, BM tại H,D
a) c/m BCHM, ACMD nội tiếp. Xác định tâm đường tròn ngoại tiếp
b) c/m CA*CB=CH*CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
27 tháng 5 2018
câu này là đề hình của 1 năm nào đó mà trong quyển ôn thi vào 10 môn toán có bn nhé! cũng không khó lắm đâu lời giải rất chi tiết hình như là đề 3 đấy (phàn đề thật)
AT
11 tháng 7 2021
AB cắt đường tròn ngoại tiếp tam giác AEK tại D
Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle EMB+\angle EHB=90+90=180\)
\(\Rightarrow EMBH\) nội tiếp \(\Rightarrow\angle KBD=\angle MBH=\angle AEH\)
Vì KEAD nội tiếp \(\Rightarrow\angle AEH=\angle KDB\Rightarrow\angle KBD=\angle KDB\)
\(\Rightarrow\Delta KDB\) cân tại K có KH là đường cao
\(\Rightarrow H\) là trung điểm BD mà B,H cố định \(\Rightarrow D\) cố định
Vì KEAD nội tiếp \(\Rightarrow I\in\) trung trực AD mà A,D cố định
\(\Rightarrow\) đpcm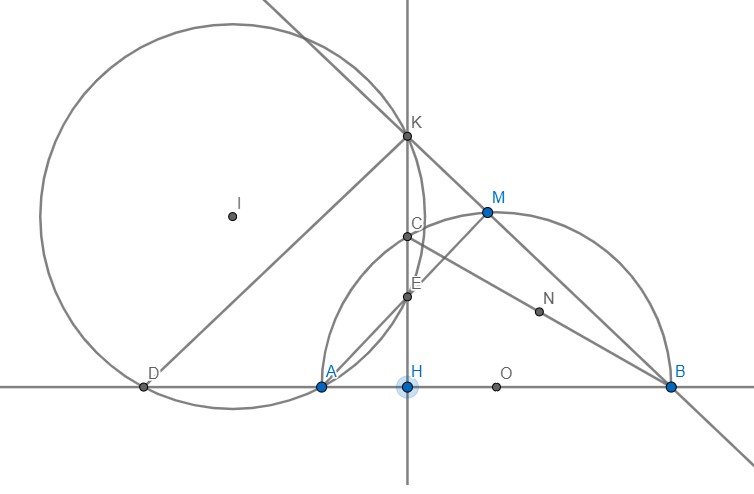
4 tháng 2 2022
a, Xét (O) có :
^AMB = 900 ( góc nt chắn nửa đường tròn )
=> ^DMA = 900
Xét tứ giác ACMD có :
^ACD = ^DMA = 900
mà 2 góc này kề nhau, cùng nhìn cạnh AD
Vậy tứ giác ACMD là tứ giác nt 1 đường tròn
b, Vì tứ giác ACMD là tứ giác nt 1 đường tròn
=> ^HNM = ^HDM ( góc nt cùng chắn cung HM ) (1)
^BNM = ^MAB ( góc nt cùng chắn cung BM ) (2)
Từ (1) ; (2) => ^HDM = ^MAB
Xét tam giác CAH và tam giác CDB có :
^ACH = ^DCB = 900
^CAH = ^CDB ( cmt )
Vậy tam giác CAH ~ tam giác CDB (g.g)
=> CA/CD = CH/BC => AC.BC = CH.CD
a: góc AMB=1/2*180=90 độ
góc HMB+góc HCB=180 độ
=>HMBC nội tiếp
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
b: Xét ΔCAH vuông tại C và ΔCDB vuông tại C có
góc CAH=góc CDB
=>ΔCAH đồng dạng với ΔCDB
=>CA/CD=CH/CB
=>CA*CB=CH*CD