Người ta thả một miếng đồng khối lượng 0,5kg vào 2 lít nước. Miếng đồng nguội từ 100C đến 25C. Hỏi nước nhận được một nhiệt lượng bằng bao nhiêu là nóng lên thêm bao nhiêu độ? (cho biết nhiệt dung của đồng là 550J/kg.K và nhiệt duy riêng của nước là 4200J/kg.K.Bỏ qua sự mất mát nhiệt do một trường)?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
14 tháng 4 2019
Nhiệt lượng nước nhận được bằng đúng nhiệt lượng do miếng đồng tỏa ra là:
Q2 = Q1 = m1.c1.(t1 - t) = 0,5.380.(80 - 20) = 11400 J
Độ tăng nhiệt độ của nước là:
H9
HT.Phong (9A5)
CTVHS
24 tháng 4 2023
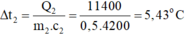
Tóm tắt:
\(m_1=0,5kg\)
\(m_2=500g=0,5kg\)
\(t_1=80^oC\)
\(t=20^oC\)
\(\Rightarrow\Delta t_1=t_1-t=80-20=60^oC\)
\(c_1=380J/kg.K\)
\(c_2=4200J/kg.K\)
===========
\(Q_2=?J\)
\(\Delta t_2=?^oC\)
Do nhiệt lượng của quả cầu tỏa ra bằng nhiệt lượng của nước nhận vào nên:
\(Q_2=Q_1=m_1.c_1.\Delta t_1=0,5.380.60=11400J\)
Nhiệt độ mà nước tăng thêm:
Theo phương trình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow11400=m_2.c_2.\Delta t_2\)
\(\Leftrightarrow\Delta t_2=\dfrac{11400}{m_2.c_2}\)
\(\Leftrightarrow\Delta t_2=\dfrac{11400}{0,5.4200}\approx5,4^oC\)
15 tháng 5 2022
Ta có phương trình cân bằng nhiệt
\(Q_{toả}=Q_{thu}\)
--> Nhiệt lượng nước nhận đc là
\(Q_{thu}=0,5.380\left(100-40\right)=11400J\)
Độ tăng nhiệt của nước
\(\Delta t=\dfrac{Q}{mc}=\dfrac{11400}{0,5.4200}=5,42^o\)
28 tháng 4 2022
Ta có pt cân bằng nhiệt
\(Q_{thu}=Q_{tỏa}\\ \Rightarrow Q_{thu}=0,5.380\left(80-20\right)=11400J\)
Nước nóng thêm số độ
\(\Delta t^o=\dfrac{Q_{thu}}{mc}=\dfrac{11400}{0,5.4200}=5,42^o\)
TC
11 tháng 5 2022
a)phương trình cân bằng nhiệt
\(Q_{thu}=Q_{tỏa}\)
\(=>Q_{thu}=m_1.c_1.\Delta t_1=0,5.380.\left(120-20\right)=19000J\)
b) nước nóng lên thêm số độ là
\(\Delta t^o=\dfrac{Q_{thu}}{m_1.c_1}=\dfrac{19000}{0,5.4200}\approx9,05^oC\)
N
2 tháng 5 2023
Cân bằng nhiệt:
\(Q_n=Q_{nhom}=mc\left(t_1-t\right)=0,5\cdot880\cdot60=26400\left(J\right)\)
Nước nóng lên thêm:
\(Q_n=mc\Delta t=0,5\cdot4200\Delta t\)
\(\Leftrightarrow26400=2100\Delta t\)
\(\Leftrightarrow\Delta t\approx12,6^0C\)
2 tháng 5 2023
Tóm tắt
\(m_1=0.5kg\\ m_2=500g=0,5kg\\ t_1=80^0C\\ t=20^0C\\ c_1=880J/kg.K\\ c_2=4200J/kg.K\\ \Rightarrow\Delta t_1=t_1-t=80-20=60^0C\)
______________
\(Q_2=?J\\ \Delta t_2=?^0C\)
Giải
Nhiệt lượng nước nhận được là:
\(Q_2=Q_1=m_1.c_1.\Delta t_1=0,5.880.60=26400J\)
Nhiệt độ mà nước nóng lên là:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\\ \Leftrightarrow0,5.880.60=0,5.4200.\Delta t_2\\ \Leftrightarrow26400=2100\Delta t_2\\ \Leftrightarrow\Delta t_2\approx12,6^0C\)
21 tháng 5 2022
Ta có phương trình cân bằng nhiệt
\(Q_{thu}=Q_{toả}=0,3.880\left(100-20\right)=21120J\\\Rightarrow \Delta t^o=\dfrac{Q_{thu}}{mc}=\dfrac{21120}{0,5.4200}\approx10^o\)
28 tháng 4 2022
Ta có phương trình cân bằng nhiệt
\(Q_{thu}=Q_{tỏa}\\ \Leftrightarrow0,5.380\left(120-20\right)=0,5.4200\left(20-t_1\right)\)
( giải pt )
\(\Rightarrow t_1=10,95238^o\approx11^o\)
nhiệt lượng tỏa ra của miếng đồng là
Q( tỏa)= 0,5.550.75
Q( tỏa )= 20625J
mà Q(thu)=Q( tỏa)
=> nhiệt lượng nước là 20625
=> Q( thu ) = 2.4200.Δt
20625=8400.Δt
Δt= 20625:8400
≃2,46 độ C
vậy nhiệt nước nóng thêm 2,46 độ C