Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1 . Tính khoảng cách d từ điểm A đến mp (BDA')
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


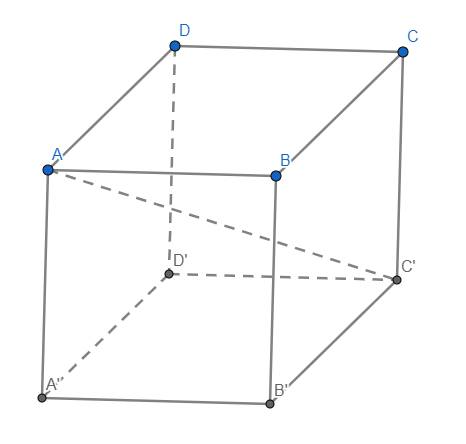
Ta có \(3AB^2=AC'^2=9a^2\) \(\Leftrightarrow AB^2=3a^2\Leftrightarrow AB=a\sqrt{3}\)
\(\Rightarrow V_{hlp}=AB^3=3a^3\sqrt{3}\) (đơn vị thể tích)

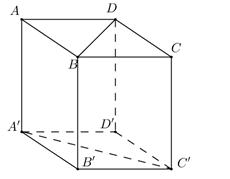
\(\overrightarrow{BD}.\overrightarrow{D'C}=\overrightarrow{BD}\left(\overrightarrow{D'D}+\overrightarrow{DC}\right)=\overrightarrow{BD}.\overrightarrow{D'D}+\overrightarrow{BD}.\overrightarrow{DC}\)
\(=\overrightarrow{BD}.\overrightarrow{DC}=-\overrightarrow{DB}.\overrightarrow{DC}=-a\sqrt{2}.a.cos45^0=-a^2\)

Đáp án C
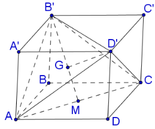
Nhận thấy chóp ACD′B′ có tất cả các
cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là
trọng tâm của tam giác AB′C′.
Chóp ACD′B′ nhận D′G là đường cao.
Xét tam giác AB′C′ có


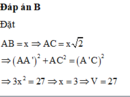
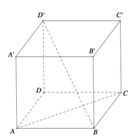
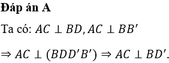



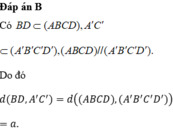
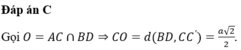
Giải chi tiết:
Dễ thấy, tứ diện A.A′BD�.�′�� có ba cạnh AB,AD,AA′��,��,��′ đôi một vuông góc.
Đặt d=d(A,(A′BD))�=�(�,(�′��)) ta có : 1d2=1AB2+1AD2+1AA′2=3⇒d=√331�2=1��2+1��2+1��′2=3⇒�=33.