dùng 20g than đá để đun 8 lít H2O.BIẾT NHIỆT DUNG RIÊNG CỦA NƯỚC LAF4200J/kg.K, NĂNG SUẤT TOẢ nhiệt của than đá là 27.10 mũ 6 j/kg, bỏ qua mọi mất mát nhiệt. Độ tăng nhiệt độ của nước là bao nhiêu?
giải giúp em với !!! <3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 4 2023
Tóm tắt
\(m_1=20g=0,02kg\\ V=8l\Rightarrow m_2=8kg\\ c=4200J/kg.K\\ q=27.10^6J/kg\)
_______________
\(\Delta t=?^0C\)
Giải
Nhiệt độ mà nước tăng thêm là:
Theo phương trình cân bằng nhiệt:
\(Q_1=Q_2\\ \Leftrightarrow m_1.q=m_2.c.\Delta t\\ \Leftrightarrow0,02.27.10^6=8.4200.\Delta t\\ \Leftrightarrow540000=33600\Delta t\\ \Leftrightarrow\Delta t=16^0C\)
24 tháng 8 2021
\(=>H=\dfrac{Qi}{Qtb}.100\%=\dfrac{25.4200\left(100-20\right)}{qm}.100\%\)
\(=>H=\dfrac{8400000}{0,5.27.10^6}.100\%=62,2\%\)
4 tháng 5 2017
\ 1 /
Tóm tắt
m1 = 120g = 0,12kg
V2 = 10l \(\Rightarrow\) m2 = 10kg
t1 = 25oC ; t2 = 100oC
c = 4200J/kg.K ; q = 44.106J/kg
H = ?
Giải
Nhiệt lượng tỏa ra khi đốt cháy hoàn toàn m1 = 0,12kg dầu hỏa (nhiệt lượng toàn phần) là:
\(Q_{tp}=m_1.q=0,12.44.10^6=5280000\left(J\right)\)
Nhiệt lượng cần cung cấp để đun sôi m2 = 10kg từ t1 = 25oC (nhiệt lượng có ích) là:
\(Q_{ci}=m_2.c\left(t_2-t_1\right)=10.4200\left(100-25\right)=3150000\left(J\right)\)
Hiệu suất của bếp dầu hỏa dùng để đun nước là:
\(H=\dfrac{Q_{tp}}{Q_{ci}}\cdot100=\dfrac{3150000}{5280000}\cdot100\approx59,66\%\)
4 tháng 5 2017
\ 2 /
Tóm tắt
m1 = 200g = 0,2kg
V2 = 8l \(\Rightarrow\) m2 = 8kg
c = 4200J/kg.K
q = 27.106J/kg
\(\Delta t=?\)
Giải
Nhiệt lượng tỏa ra khi đốt cháy hoàn toàn m1 = 0,2kg than đá là:
\(Q_{tỏa}=m_1.q=0,2.27.10^6=5400000\left(J\right)\)
Do bỏ qua mọi dự mất mát nhiệt nên toàn bộ nhiệt lượng trên được truyền vào cho nước và làm nước nóng lên. Ta có:
\(Q_{tỏa}=Q_{thu}\\ \Rightarrow5400000=m_2.c.\Delta t\\ \Rightarrow5400000=33600\Delta t\\ \Rightarrow\Delta t=160\left(^oC\right)\)
21 tháng 4 2017
tóm tắt:
\(V_{nước}=2l\Rightarrow m_{nước}=2kg\\ t_2=25^0C\\ t_2=100^0C\\ c_{nước}=4200\dfrac{J}{Kg.K}\\ q_{tb}=14\cdot10^6\dfrac{J}{kg}\\ m_{tb}=?\)
Nhiệt lượng cần thiết đẻ đun sô nước là:
\(Q=m_{nước}\cdot c_{nước}\cdot\Delta t=m_{nước}\cdot c_{nước}\cdot\left(t_2-t_1\right)\\ =2\cdot4200\cdot\left(100-25\right)=630000\left(J\right)\)
Khối lượng than bùn cần dùng là
ta có: \(Q=q_{tb}\cdot m_{tb}\Rightarrow m_{tb}=\dfrac{Q}{q_{tb}}=\dfrac{630000}{14\cdot10^6}=0,045\left(kg\right)\)
Vậy cần 0,045kg than bùn để đun nóng nước
VT
25 tháng 11 2019
Đáp án: D
- Nhiệt lượng ấm nhôm thu vào để nóng đến 100 0 C là:
Q 1 = m 1 . C 1 . ∆ t 1 = 0,3. 880. (100 – 30) = 18480 (J)
- Nhiệt lượng cần đun sôi nước là:
Q 2 = m 2 . C 2 . ∆ t = 2,5.4200. (100 – 20) = 840000 (J)
- Nhiệt lượng toả ra khi đốt cháy hoàn toàn 0,2 kg củi là:
Q t ỏ a = m. q = 0,2. 10 7 = 2 000 000 (J)
- Nhiệt lượng tỏa ra môi trường là:
∆ Q = Q 2 - Q 1 = 2000000 - 840000 - 181480 = 1141520(J)
VT
9 tháng 10 2019
Gọi λ là nhiệt nóng chảy riêng của cục nước đá khối lượng m 0 ở t 0 = 0 ° C ; còn c 1 , m 1 , c 2 , m 2 là nhiệt dung riêng và khối lượng của cốc nhôm và của lượng nước đựng trong cốc ở nhiệt độ t 1 = 20 ° C. Nếu gọi t ° C là nhiệt độ của nước trong cốc nhôm khi cục nước đá vừa tan hết thì lượng nhiệt do cục nước đá ở t 0 = 0 ° C đã thu vào để tan thành nước ở t ° C bằng :
Q = λ m 0 + c 2 m 0 (t - t 0 ) = m 0 ( λ + c 2 t)
Còn nhiệt lượng do cốc nhôm và lượng nước đựng trong cốc ở t 1 = 20 ° C. toả ra để nhiệt độ của chúng giảm tới toC (với t < t 1 ) có giá trị bằng :
Q'= ( c 1 m 1 + c 2 m 2 )( t 1 - t)
Theo định luật bảo toàn năng lượng, ta có :
Q' = Q ⇒ ( c 1 m 1 + c 2 m 2 ) ( t 1 - t) = m 0 ( λ + c 2 t)
Từ đó suy ra :
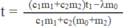
Thay số : t ≈ 3,7 ° C.
VT
26 tháng 6 2018
Đáp án: B
- Nhiệt lượng cần thiết để đun ấm nước:
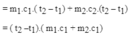
- Thay số vào ta được:
- Năng lượng do bếp tỏa ra ( năng suất tỏa nhiệt):
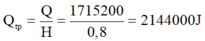
- Khối lượng dầu cần dùng là:
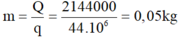
- Thể tích dầu hỏa đã dùng là:
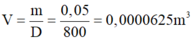
= 62 , 5 c m 3
dùng 20g than đá để đun sôi 8 lít H2O à bạn
Tóm tắt:
\(m_1=20g=0,02kg\)
\(V=8l\Rightarrow m_2=8kg\)
\(c=4200J/kg.k\)
\(q=27.10^6J/kg\)
===========
\(\Delta t=?^oC\)
Độ tăng nhiệt độ của nước là:
\(Q=q.m_1\)
\(\Leftrightarrow m_2.c.\Delta t=q.m_1\)
\(\Leftrightarrow8.4200.\Delta t=0,02.27.10^6\)
\(\Leftrightarrow33600\Delta t=540000\)
\(\Leftrightarrow\Delta t=\dfrac{540000}{33600}\approx16,1^oC\)