có một hộp đựng 5 viên bi xanh ,6 viên bi đỏ và 4 viên bi vàng a)có bao nhiêu cách lấy ra 6 viên bi ,trong đó có 2 viên bi xanh và có nhiều nhất 2 viên bi vàng và phải có đủ 3 màu. b)có bao nhiêu cách lấy ra 9 viên bi đủ 3...
Đọc tiếp
có một hộp đựng 5 viên bi xanh ,6 viên bi đỏ và 4 viên bi vàng a)có bao nhiêu cách lấy ra 6 viên bi ,trong đó có 2 viên bi xanh và có nhiều nhất 2 viên bi vàng và phải có đủ 3 màu. b)có bao nhiêu cách lấy ra 9 viên bi đủ 3 màu
cách.
cách.
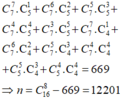
a: Số cách chọn là:
\(C^2_5\cdot C^1_4\cdot C^3_6+C^2_5\cdot C^2_4\cdot C^2_6=1700\left(cách\right)\)
b: Số cách chọn 9 viên bất kì là: \(C^9_{15}\left(cách\right)\)
Số cách chọn 9 viên ko có đủ 3 màu là:
\(C^9_9+C^9_{11}+C^9_{10}=66\left(cách\right)\)
=>Có 4939 cách