Cho hàm số y = cot2x. Chọn khẳng định đúng:
A. y' - 2y2 + 2 = 0
B. 2y' + y2 + 2 = 0
C. y' + 2y + 2 = 0
D. 2y' - y2 + 2 = 0
Giải thích rõ dùm mình với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Hàm số y = x 4 − 3 x 2 + 2 có a,b trái dấu và a>0 nên hàm số có 2 cực tiểu và 1 cực đại.

Đáp án C
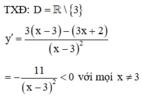
Vậy hàm số nghịch biến trên các khoảng - ∞ ; 3 và 3 ; + ∞

Đáp án D
Ta có y ' = − 3 x 2 + 6 x = − 3 x x − 2 ⇒ y ' > 0 ⇔ 0 < x < 2 y ' < 0 ⇔ x > 2 x < 0
Suy ra hàm số đồng biến trên khoảng (0;2), nghịch biến trên các khoảng − ∞ ; 0 và 2 ; + ∞

Đáp án C
y = x 3 + 3 x 2 − 9 x − 2017 ⇒ y ' = 3 x 2 + 6 x − 9 ; y ' = 0 ⇔ x = 1 x = − 3
Dễ thấy hàm số đạt cực đại tại x=-3; đạt cực tiểu tại x=1.

Đáp án B
Tập xác định ℝ \ 4
Ta có y ' = 3 4 − x 2 > 0 , ∀ x ≠ 4 , nên hàm số đồng biến trên mỗi khoảng xác định của nó.
\(y'=-\dfrac{2}{sin^22x}=-2\left(1+cot^22x\right)=-2-2cot^22x=-2-2y^2\)
\(\Rightarrow y'+2y^2+2=0\)
Cả 4 đáp án đều sai