Question

[Hồ Quang Hưng]

Cho tam giác ABC nhọn nội tiếp đường tròn (O). OM vuông góc AB, ON vuông góc AC (M thuộc AB, N thuộc AC).

1) CM tứ giác AMON nội tiếp.

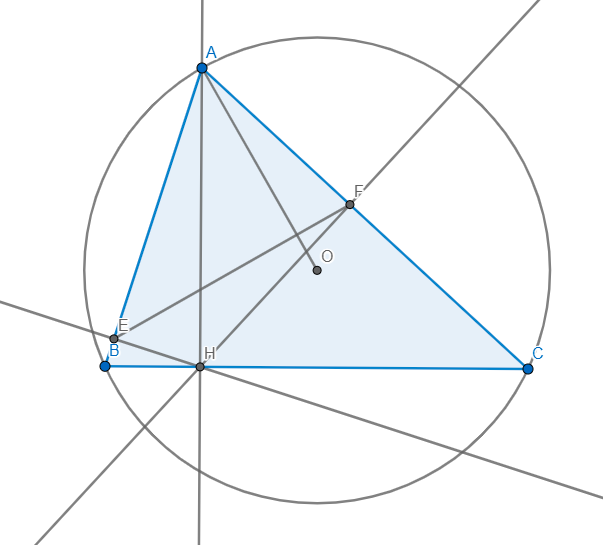
2) AH vuông góc BC tại H. I là trung điểm AO. Dây AE đường tròn tâm I đường kính AO sao cho AE // BC. HE cắt MN tại K. CM IK vuông góc BC.

3) HE cắt đường tròn tâm I đường kính AO tại D. CM DM là tia phân giác góc BDE.

Answer 1

[Nguyễn Lê Phước Thịnh]

1: góc AMO+góc ANO=180 độ

=>AMON nội tiếp

2: ΔOAB cân tại O

mà OM là đường cao

nên M là trung điểm của AB

ΔOAC cân tại O

mà ON là đường cao

nên N là trung điểm của AC

=>NM là đừog trung bình

=>MN//BC

=>MN//AE

=>AMNE là hình thang cân

=>AM=EN; AN=EM

ΔAHB vuông tại H có HM là trung tuyến

nên HM=AB/2=MA=MB

ΔHAC vuông tại H có HN là trung tuyến

nên HN=AN=CN=AC/2

=>HM=EN; HN=EM

=>HMEN là hình bbình hành

=>K làtrung điểm của MN

=>IK vuông góc MN

=>IK vuông góc BC

3: goc MDE+gó MDH=180 độ

=>góc MDE=góc MBH

=>BMDH nội tiếp

=>góc MDB=góc MHB=góc MBH

=>góc MDB=góc MDE

=>DM là phân giác của góc BDE