Cho ΔABC cân tại A. Vẽ hai đường trung tuyến BM và CN cắt nhau tại I.
a) Chứng minh: ΔABM = ΔACN
b) Gọi H là giao điểm của AI và BC. Chứng minh: AH⊥BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 4 2022
a. +) Tam giác ABC cân tại A:
=> góc B = góc C
=> AB = AC
=> AM + BM = AN + CN
mà BM và CN là 2 đường trung tuyến của AB và AC
=> AM = BM = AN = CN
Xét tam giác BNC và tam giác CMB:
BM = CN (cmt)
góc B = góc C (cmt)
BC chung
=> tam giác BNC = tam giác CMB (c-g-c)
+) Ta có: BM , CN là 2 đường trung tuyến của tam giác ABC, cắt nhau tại I
=> I là trọng tâm của tam giác ABC
=> BI = \(\dfrac{2}{3}BM\)
CI = \(\dfrac{2}{3}CN\)
mà BM = CN
=> BI = CI
=> tam giác BIC cân tại I (đpcm)
b. +)Xét tam giác AIB và tam giác AIC:
AI chung
AB = AC
BI = CI
=> tam giác AIB = tam giác AIC (c-c-c)
=> góc BAI = góc CAI (2 góc tương ứng)
=> AI là tia phân giác góc A (1)
+) Xét tam giác AKB và tam giác AKC:
AK chung
AB = AC
BK = CK (vì K là trung điểm BC)
=> tam giác AKB = tam giác AKC (c-c-c)
=> AK là tia phân giác góc A (2)
Từ (1) và (2) , suy ra:
AI trùng AK
=> A, I, K thẳng hàng
8 tháng 5 2022
a. vì tam giác ABC cân tại A
=> AB = AC
=> góc ABC = góc ACB
BM và CN là 2 đường trung tuyến của tam giác ABC
=> N và M lần lượt là trung điểm của AB và AC
=> AN = BN
AM = CM
mà AB = AC
=> AN = BN = AM = CM
Xét tam giác BNC và tam giác CMB:
BC chung
góc ABC = góc ACB (cmt)
BN = CM (cmt)
=> tam giác BNC = tam giác CMB (c-g-c) (đpcm)
b. tam giác BNC = tam giác CMB (cmt)
=> BM = CN ( 2 cạnh tương ứng)
mà BM giao CN tại K
=> K là trọng tâm của tam giác ABC
=> BK = CK
Xét Δ AKB và Δ AKC:
AK chung
AB = AC (cmt)
BK = CK (cmt)
=> Δ AKB = Δ AKC (c-c-c)
=> góc BAK = góc CAK (2 góc tương ứng)
=> AK là tia phân giác góc BAC
=> AK là đường trung trực của Δ ABC
=> AK ⊥ BC (đpcm)
c. Vì AK (AH) ⊥ BC
=> tam giác ABH vuông tại H
mà AH là đường trung trực của tam giác ABC
=> BH = CH = \(\dfrac{BC}{2}=\dfrac{6}{2}=3cm\)
Áp dùng định lí Py - ta - go vào tam giác ABH:
AB2 = BH2 + AH2
52 = 32 + AH2
AH2 = 52 - 32 = 25 - 9 = 16
=> AK = 4cm (AH > 0)
21 tháng 9 2023
Tham khảo:
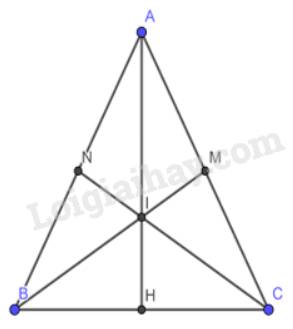
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC
24 tháng 4 2023
b: Xét tứ giác ABCE có
M là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>CE//AB
c: Xét ΔHAB vuông tại H và ΔHKC vuông tại H có
HB=HC
góc HAB=góc HKC
=>ΔHAB=ΔHKC
=>HA=HK
Xét tứ giác ABKC có
H là trung điểm chung của BC và AK
AB=AC
=>ABKC là hình thoi
=>AC=CK
Xét ΔABC có
BM,AH là trung tuyến
BM cắt AH tại G
=>G là trọng tâm
=>3GH=AH
3GH+HC=AH+HC>AC=CK
14 tháng 4 2023
a;
có Abc là tam giac cân taji A (gt)
=> AH là đg cao và là ddg trùng tuyến và là đg phan giác
=> H là trung điểm của BC
Xét tam giác ABH va ACH có
1: có AH chung
2: HB=HC( CMT)
3: AB=AC (2 cạnh bên của tam giác ABC cân tại a)
=> 2 tam giác bằng nhau theo TH c.c.c
b;
xét 2 tam giác: AMB va CME có
AM=MC ( BM là trung tuyến=>m là trung điểm AC)
MB=ME (GT)
Góc AMB=Goc AMC (2 góc đối đỉnh)
=> 2tam giác bằng nhau theo TH (CGC)
=> góc CEm= góc ABM (2 góc tương ung trong 2 tam giác bằng nhau)
=> AB//CE (2 đg thằng có 2 góc đồng vị bằng nhau)
c;
có AB//CE (CMt)
=> Góc ABC= góc BCK (2 góc so le trong)
xet 2 tam giác vuông ACH va KCH có
HC chung
goc KCH=ACH (cùng bằng góc ABC)
=> 2 tam giác bằng nhau
=>HK=AH (1)
xet Tam gioác ABC có am là trung tuyên tại M; BM là trung tuyến
=> G là trọng tâm
=> HG= 1/3 AH (tinh chât trọng tâm của tam giác) (2)
tù 1 và 2 => HG=1/3 HK => HK=3HG(3)
Trong Tam giác KHC có
CK< HC+HK (4)
Từ 3 và 4 => KC< HC+3HG (dieu phai chung minh)
27 tháng 3 2022
a) Xét \(\Delta AHB\) vuông tại H và \(\Delta AHC\) vuông tại H:
AB = AC (\(\Delta ABC\) cân tại A).
\(\widehat{B}=\widehat{C}\) (\(\Delta ABC\) cân tại A).
\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - góc nhọn).
b) Xét \(\Delta DHC:\)
DI là trung tuyến (I là trung điểm của HC).
DI là đường cao \(\left(DI\perp HC\right).\)
\(\Rightarrow\Delta DHC\) cân tại D.
a: Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
b: Xét ΔABC có
BM,CN là trung tuyến
BM cắt CN tại I
=>I là trọng tam
=>H là trung điểm của BC
ΔABC cân tại A
mà AH là trung tuyến
nên AH vuông góc BC