Rút gọn biểu thức: A = \(\dfrac{10\sqrt{x}}{x+3\sqrt{x}-4}\) - \(\dfrac{2\sqrt{x}-3}{\sqrt{x}+4}\) + \(\dfrac{\sqrt{x}+1}{1-\sqrt{x}}\) ( Với x \(\ge\) 0, x \(\ne\) 1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2021
`A=(2\sqrtx-9)(x-5sqrtx+6)-(sqrtx+3)/(sqrtx-2)-(2sqrtx+1)(3-sqrtx)(x>=0,x ne 4, x ne 9)`
`=(2\sqrtx-9)(x-5sqrtx+6)-(sqrtx+3)/(sqrtx-2)+(2sqrtx+1)(sqrtx-3)`
`=(2sqrtx-9-x+9+2x-3sqrtx-2)/(x-5sqrtx+6)`
`=(x-sqrtx-2)/(x-5sqrtx+6)`
`=((\sqrtx+1)(sqrtx-2))/((sqrtx-2)(sqrtx-3))`
`=(sqrtx+1)/(sqrtx-3)`
16 tháng 5 2021
`A=(2\sqrtx-9)/(x-5sqrtx+6)-(sqrtx+3)/(sqrtx-2)-(2sqrtx+1)/(3-sqrtx)(x>=0,x ne 4, x ne 9)`
`=(2\sqrtx-9)/(x-5sqrtx+6)-(sqrtx+3)/(sqrtx-2)+(2sqrtx+1)/(sqrtx-3)`
`=(2sqrtx-9-x+9+2x-3sqrtx-2)/(x-5sqrtx+6)`
`=(x-sqrtx-2)/(x-5sqrtx+6)`
`=((\sqrtx+1)(sqrtx-2))/((sqrtx-2)(sqrtx-3))`
`=(sqrtx+1)/(sqrtx-3)`
14 tháng 10 2021
\(a,A=4\sqrt{3}-5\sqrt{3}+2-\sqrt{3}=2-2\sqrt{3}\\ B=\dfrac{x+2\sqrt{x}+8+2\sqrt{x}-8}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+4\right)}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-4}\\ b,B-\dfrac{1}{2}A=\dfrac{\sqrt{x}}{\sqrt{x}-4}-\dfrac{1}{2}\left(2-2\sqrt{3}\right)=0\\ \Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-4}=1+\sqrt{3}\\ \Leftrightarrow\sqrt{x}=\left(1+\sqrt{3}\right)\left(\sqrt{x}-4\right)\Leftrightarrow\sqrt{x}=\sqrt{x}-4\sqrt{3}+\sqrt{3x}-4\\ \Leftrightarrow\sqrt{3x}=4\sqrt{3}+4\\ \Leftrightarrow\sqrt{x}=\dfrac{4\sqrt{3}+4}{\sqrt{3}}\\ \Leftrightarrow\sqrt{x}=\dfrac{12+4\sqrt{3}}{3}\\ \Leftrightarrow x=\dfrac{192+96\sqrt{3}}{9}=\dfrac{64+32\sqrt{3}}{3}\)
28 tháng 8 2023
a:
Sửa đề: \(P=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{3x+3}{9-x}\right)\cdot\left(\dfrac{\sqrt{x}-7}{\sqrt{x}+1}+1\right)\)
\(P=\left(\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{x-9}\right)\cdot\dfrac{\sqrt{x}-7+\sqrt{x}+1}{\sqrt{x}+1}\)
\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{x-9}\cdot\dfrac{2\sqrt{x}-6}{\sqrt{x}+1}\)
\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{2}{\sqrt{x}+1}=\dfrac{-6}{\sqrt{x}+3}\)
b: P>=1/2
=>P-1/2>=0
=>\(\dfrac{-6}{\sqrt{x}+3}-\dfrac{1}{2}>=0\)
=>\(\dfrac{-12-\sqrt{x}-3}{2\left(\sqrt{x}+3\right)}>=0\)
=>\(-\sqrt{x}-15>=0\)
=>\(-\sqrt{x}>=15\)
=>căn x<=-15
=>\(x\in\varnothing\)
c: căn x+3>=3
=>6/căn x+3<=6/3=2
=>P>=-2
Dấu = xảy ra khi x=0
DM
8 tháng 8 2021
a) \(P=\dfrac{1}{2-\sqrt{3}}+\dfrac{1}{2+\sqrt{3}}\)
\(=\dfrac{2+\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}+\dfrac{2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\dfrac{2+\sqrt{3}+2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\dfrac{4}{4-3}\)
\(=4\)
b) \(Q=\left(1+\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\right).\dfrac{1}{\sqrt{x}}vớix>0,x\ne4\)
\(=\left(\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\sqrt{x}-2}\right).\dfrac{1}{\sqrt{x}}\)
\(=\)\(\dfrac{2\sqrt{x}}{\sqrt{x}-2}.\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2}{\sqrt{x}-2}\)
7 tháng 11 2021
\(a,A=\dfrac{2\cdot2-4}{2-1}=0\\ b,B=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ B=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\\ c,AB=\dfrac{2\sqrt{x}-4}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{2\sqrt{x}-4}{\sqrt{x}+1}=\dfrac{5\left(\sqrt{x}+1\right)-3\left(\sqrt{x}+3\right)}{\sqrt{x}+1}\\ AB=5-\dfrac{3\left(\sqrt{x}+3\right)}{\sqrt{x}+1}\)
Vì \(\dfrac{3\left(\sqrt{x}+3\right)}{\sqrt{x}+1}>0\) nên \(AB< 5\)
7 tháng 11 2021
a. \(x=4\Rightarrow A=\dfrac{2.\sqrt{4}-4}{\sqrt{4}-1}=0\)
b. \(\Rightarrow B=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-\left(6\sqrt{x}-4\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow B=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow B=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow B=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
1 tháng 2 2022
a, \(A=\dfrac{4\left(3-\sqrt{7}\right)}{2}+2\sqrt{7}=\dfrac{12}{2}=6\)
b, \(B=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}}\right):\dfrac{2-\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\dfrac{2-\sqrt{x}}{x-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
1 tháng 2 2022
nhờ bạn làm rõ vì sao \(\dfrac{\sqrt{x}-2\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{2-\sqrt{x}}{x-1}\) lại bằng \(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
mình xin cảm ơn
AT
12 tháng 7 2021
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-6\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x-2\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
\(A< \dfrac{3}{5}\Rightarrow\dfrac{3}{5}-A>0\Rightarrow\dfrac{3}{5}-\dfrac{\sqrt{x}-3}{\sqrt{x}-1}>0\)
\(\Rightarrow\dfrac{3\left(\sqrt{x}-1\right)-5\left(\sqrt{x}-3\right)}{5\left(\sqrt{x}-1\right)}>0\Rightarrow\dfrac{12-2\sqrt{x}}{5\left(\sqrt{x}-1\right)}>0\)
\(\Rightarrow\dfrac{2}{5}.\dfrac{6-\sqrt{x}}{\sqrt{x}-1}>0\Rightarrow\dfrac{6-\sqrt{x}}{\sqrt{x}-1}>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}6-\sqrt{x}>0\\\sqrt{x}-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}6-\sqrt{x}< 0\\\sqrt{x}-1< 0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}1< x< 36\\\left\{{}\begin{matrix}x>36\\x< 1\end{matrix}\right.\left(l\right)\end{matrix}\right.\)
\(\Rightarrow1< x< 36\)
12 tháng 7 2021
\(=>A=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-6\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(A=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(A=\dfrac{x-2\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(A=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
để \(A< \dfrac{3}{5}< =>\dfrac{\sqrt{x}-3}{\sqrt{x}-1}< \dfrac{3}{5}\)
\(< =>\dfrac{5\left(\sqrt{x}-3\right)-3\left(\sqrt{x}-1\right)}{5\left(\sqrt{x}-1\right)}< 0\)
\(< =>\dfrac{2\sqrt{x}-12}{5\left(\sqrt{x}-1\right)}< 0\)
\(=>\left\{{}\begin{matrix}\left[{}\begin{matrix}2\sqrt{x}-12>0\\5\left(\sqrt{x}-1\right)< 0\end{matrix}\right.\\\left[{}\begin{matrix}2\sqrt{x}-12< 0\\5\left(\sqrt{x}-1\right)>0\end{matrix}\right.\end{matrix}\right.\)\(=>\left\{{}\begin{matrix}\left[{}\begin{matrix}x>36\\x< 1\end{matrix}\right.\\\left[{}\begin{matrix}x< 36\\x>1\end{matrix}\right.\end{matrix}\right.=>1< x< 36\left(tm\right)\)
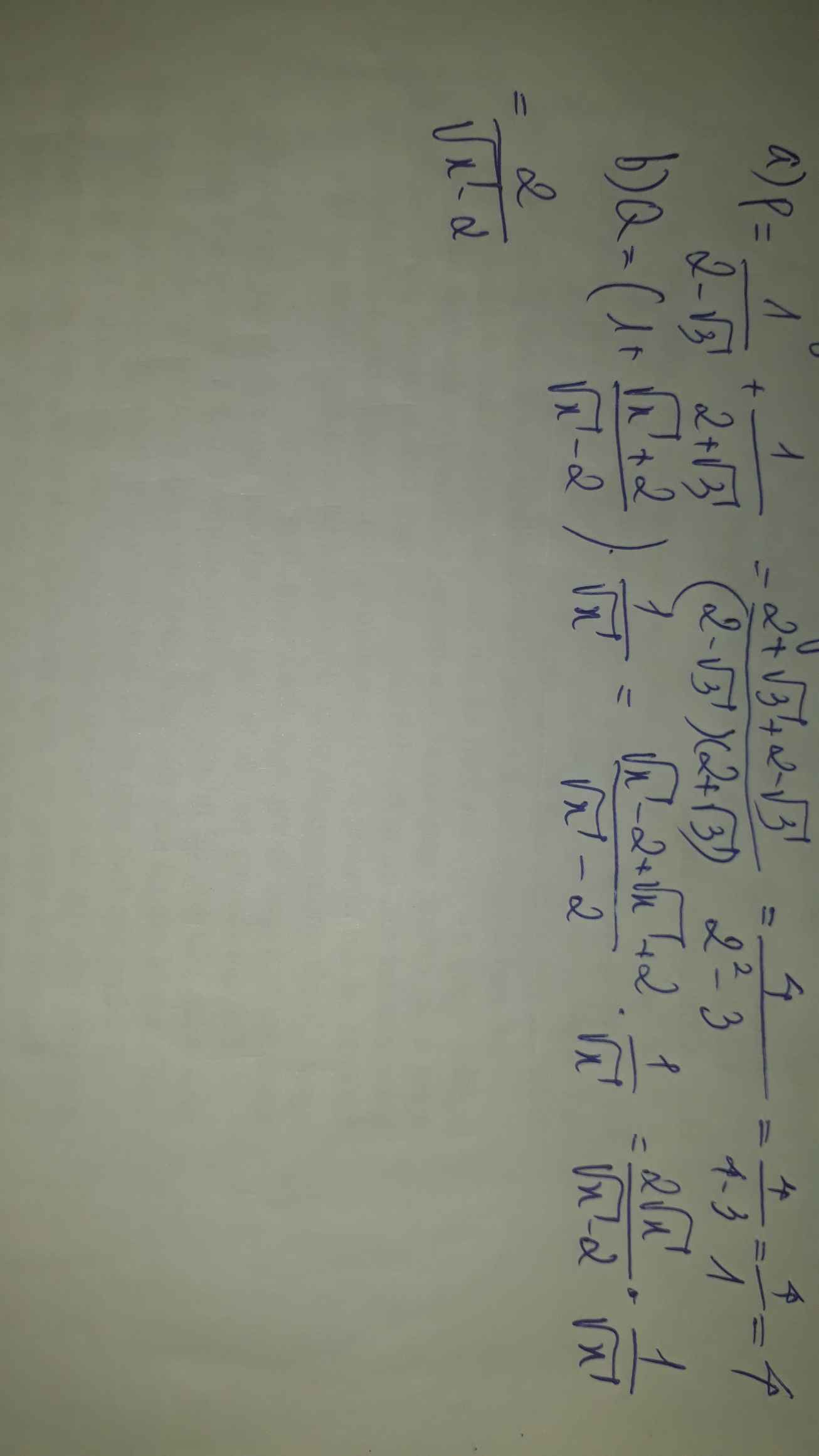
Lời giải:
$A=\frac{10\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+4)}-\frac{(2\sqrt{x}-3)(\sqrt{x}-1)}{(\sqrt{x}+4)(\sqrt{x}-1)}-\frac{(\sqrt{x}+1)(\sqrt{x}+4)}{(\sqrt{x}-1)(\sqrt{x}+4)}$
$=\frac{10\sqrt{x}-(2\sqrt{x}-3)(\sqrt{x}-1)-(\sqrt{x}+1)(\sqrt{x}+4)}{(\sqrt{x}+4)(\sqrt{x}-1)}$
$=\frac{-3x+10\sqrt{x}-7}{(\sqrt{x}+4)(\sqrt{x}-1)}$
$=\frac{-(\sqrt{x}-1)(3\sqrt{x}-7)}{(\sqrt{x}+4)(\sqrt{x}-1)}=\frac{7-3\sqrt{x}}{\sqrt{x}+4}$