2x+1=5 .Tìm x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ta có: \(\left(2x-5\right)\left(x+2\right)-2x\left(x-1\right)=15\)
\(\Leftrightarrow2x^2+4x-5x-10-2x^2+2x=15\)
\(\Leftrightarrow x=25\)
b: Ta có: \(\left(5-2x\right)\left(2x+7\right)=4x^2-25\)
\(\Leftrightarrow4x^2-25+\left(2x-5\right)\left(2x+7\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(2x+5+2x+7\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-3\end{matrix}\right.\)
c: Ta có: \(x\left(4x-5\right)-\left(2x+1\right)^2=0\)
\(\Leftrightarrow4x^2-5x-4x^2-4x-1=0\)
\(\Leftrightarrow-9x=1\)
hay \(x=-\dfrac{1}{9}\)

`@` `\text {Ans}`
`\downarrow`
\(\dfrac{x-3}{3}=\dfrac{2x+1}{5}\)
`=> (x-3)5 = (2x+1)3`
`=> 5x-15 = 6x+3`
`=> 5x-6x = 15+3`
`=> -x=18`
`=> x=-18`
\(\dfrac{x+1}{22}=\dfrac{6}{x}\)
`=> (x+1)x = 22*6`
`=> (x+1)x = 132`
`=> x^2 + x = 132`
`=> x^2+x-132=0`
`=> (x-11)(x+12)=0`
`=>`\(\left[{}\begin{matrix}x-11=0\\x+12=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=11\\x=-12\end{matrix}\right.\)
\(\dfrac{2x-1}{2}=\dfrac{5}{x}\)
`=> (2x-1)x = 2*5`
`=> 2x^2 - x =10`
`=> 2x^2 - x - 10 =0`
`=> 2x^2 + 4x - 5x - 10 =0`
`=> (2x^2 + 4x) - (5x+10)=0`
`=> 2x(x+2) - 5(x+2)=0`
`=> (2x-5)(x+2)=0`
`=>`\(\left[{}\begin{matrix}2x-5=0\\x+2=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}2x=5\\x=-2\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\end{matrix}\right.\)
\(\dfrac{2x-1}{21}=\dfrac{3}{2x+1}\)
`=> (2x-1)(2x+1)=21*3`
`=> 4x^2 + 2x - 2x - 1 = 63`
`=> 4x^2 - 1=63`
`=> 4x^2 - 1 - 63=0`
`=> 4x^2 - 64 = 0`
`=> 4(x^2 - 16)=0`
`=> 4(x^2 + 4x - 4x - 16)=0`
`=> 4[(x^2+4x)-(4x+16)]=0`
`=> 4[x(x+4)-4(x+4)]=0`
`=> 4(x-4)(x+4)=0`
`=>`\(\left[{}\begin{matrix}x-4=0\\x+4=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
\(\dfrac{2x+1}{9}=\dfrac{5}{x+1}\)
`=> (2x+1)(x+1) = 9*5`
`=> (2x+1)(x+1)=45`
`=> 2x^2 + 2x + x + 1 = 45`
`=> 2x^2 + 3x + 1 =45`
`=> 2x^2 + 3x + 1 - 45 =0`
`=> 2x^2+3x-44=0`
`=> 2x^2 + 11x - 8x - 44=0`
`=> (2x^2 +11x) - (8x+44)=0`
`=> x(2x+11) - 4(2x+11)=0`
`=> (x-4)(2x+11)=0`
`=>`\(\left[{}\begin{matrix}x-4=0\\2x+11=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=4\\2x=-11\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=4\\x=-\dfrac{11}{2}\end{matrix}\right.\)
\(\dfrac{x-3}{3}=\dfrac{2x+1}{5}\\ \left(x-3\right)\cdot5=\left(2x+1\right)\cdot3\\ x5-15=6x+3\\ x5-6x=3+15\\ -x=18\\ \Rightarrow x=-18\)
\(\dfrac{x+1}{22}=\dfrac{6}{x}\\ \left(x+1\right)\cdot x=6\cdot22\\ \left(x+1\right)\cdot x=2\cdot3\cdot2\cdot11\\ \left(x+1\right)\cdot x=12\cdot11\\ \Rightarrow x=11\)
\(\dfrac{2x-1}{21}=\dfrac{3}{2x+1}\\ \left(2x-1\right)\cdot\left(2x+1\right)=21\cdot3\\ \left(2x-1\right)\cdot\left(2x+1\right)=7\cdot3\cdot3\\ \left(2x-1\right)\cdot\left(2x+1\right)=7\cdot9\\ \Rightarrow2x+1=9\\ 2x=8\\ x=4\)

a) Ta có: \(6x\left(x-5\right)+3x\left(7-2x\right)=18\)
\(\Leftrightarrow6x^2-30x+21x-6x^2=18\)
\(\Leftrightarrow-9x=18\)
hay x=-2
Vậy: S={-2}
b) Ta có: \(2x\left(3x+1\right)+\left(4-2x\right)\cdot3x=7\)
\(\Leftrightarrow6x^2+2x+12x-6x^2=7\)
\(\Leftrightarrow14x=7\)
hay \(x=\dfrac{1}{2}\)
Vậy: \(S=\left\{\dfrac{1}{2}\right\}\)
c) Ta có: \(0.5x\left(0.4-4x\right)+\left(2x+5\right)\cdot x=-6.5\)
\(\Leftrightarrow0.2x-2x^2+2x^2+5x=-6.5\)
\(\Leftrightarrow5.2x=-6.5\)
hay \(x=-\dfrac{5}{4}\)
Vậy: \(S=\left\{-\dfrac{5}{4}\right\}\)
d) Ta có: \(\left(x+3\right)\left(x+2\right)-\left(x-2\right)\left(x+5\right)=6\)
\(\Leftrightarrow x^2+5x+6-\left(x^2+3x-10\right)=6\)
\(\Leftrightarrow x^2+5x+6-x^2-3x+10=6\)
\(\Leftrightarrow2x+16=6\)
\(\Leftrightarrow2x=-10\)
hay x=-5
Vậy: S={-5}
e) Ta có: \(3\left(2x-1\right)\left(3x-1\right)-\left(2x-3\right)\left(9x-1\right)=0\)
\(\Leftrightarrow3\left(6x^2-5x+1\right)-\left(18x^2-29x+3\right)=0\)
\(\Leftrightarrow18x^2-15x+3-18x^2+29x-3=0\)
\(\Leftrightarrow14x=0\)
hay x=0
Vậy: S={0}

Tìm x
a) (12x-5)(3x-1)-(18x-1)(2x+3)=5
b) (x+2)(x-3)-(x-2)(x+5)=2(x+3)
c) (2x+3)(2x-1)-(2x+5)-(2x-3)=12


a) Ta có: \(\dfrac{1}{4}-\left|x+\dfrac{1}{2}\right|=\dfrac{1}{8}\)
\(\Leftrightarrow\left|x+\dfrac{1}{2}\right|=\dfrac{1}{8}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{1}{8}\\x+\dfrac{1}{2}=-\dfrac{1}{8}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3}{8}\\x=\dfrac{-5}{8}\end{matrix}\right.\)

a: \(2x\left(x-1\right)-x\left(2x-5\right)=9\)
=>\(2x^2-2x-2x^2+5x=9\)
=>3x=9
=>\(x=\dfrac{9}{3}=3\)
b: \(\left(3x-2\right)^2-5\left(x-1\right)\left(x+2\right)=\left(2x-3\right)^2\)
=>\(9x^2-12x+4-5\left(x^2+x-2\right)=4x^2-12x+9\)
=>\(9x^2-12x+4-5x^2-5x+10=4x^2-12x+9\)
=>\(4x^2-17x+14=4x^2-12x+9\)
=>\(-17x+14=-12x+9\)
=>\(-5x=-5\)
=>x=1

√(x² + x + 1) = 1
⇔ x² + x + 1 = 1
⇔ x² + x = 0
⇔ x(x + 1) = 0
⇔ x = 0 hoặc x + 1 = 0
*) x + 1 = 0
⇔ x = -1
Vậy x = 0; x = -1
--------------------
√(x² + 1) = -3
Do x² ≥ 0 với mọi x
⇒ x² + 1 > 0 với mọi x
⇒ x² + 1 = -3 là vô lý
Vậy không tìm được x thỏa mãn yêu cầu
--------------------
√(x² - 10x + 25) = 7 - 2x
⇔ √(x - 5)² = 7 - 2x
⇔ |x - 5| = 7 - 2x (1)
*) Với x ≥ 5, ta có
(1) ⇔ x - 5 = 7 - 2x
⇔ x + 2x = 7 + 5
⇔ 3x = 12
⇔ x = 4 (loại)
*) Với x < 5, ta có:
(1) ⇔ 5 - x = 7 - 2x
⇔ -x + 2x = 7 - 5
⇔ x = 2 (nhận)
Vậy x = 2
--------------------
√(2x + 5) = 5
⇔ 2x + 5 = 25
⇔ 2x = 20
⇔ x = 20 : 2
⇔ x = 10
Vậy x = 10
-------------------
√(x² - 4x + 4) - 2x +5 = 0
⇔ √(x - 2)² - 2x + 5 = 0
⇔ |x - 2| - 2x + 5 = 0 (2)
*) Với x ≥ 2, ta có:
(2) ⇔ x - 2 - 2x + 5 = 0
⇔ -x + 3 = 0
⇔ x = 3 (nhận)
*) Với x < 2, ta có:
(2) ⇔ 2 - x - 2x + 5 = 0
⇔ -3x + 7 = 0
⇔ 3x = 7
⇔ x = 7/3 (loại)
Vậy x = 3
1)
\(\Leftrightarrow x^2+x+1=1^2=1\\ \Leftrightarrow x^2+x=0\\ \Leftrightarrow x\left(x+1\right)=0\\ \Rightarrow\left\{{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
2) Do \(x^2+1>0\forall x\) nên \(x\in\varnothing\)
3)
\(\Leftrightarrow\sqrt{\left(x-5\right)^2}=7-2x\\ \Leftrightarrow\left|x-5\right|=7-2x\)
Nếu \(x\ge5\) thì
\(\Leftrightarrow x-5-7+2x=0\\ \Leftrightarrow3x-12=0\\ \Leftrightarrow3x=12\\ \Rightarrow x=4\)
=> Loại trường hợp này
Nếu \(x< 5\) thì
\(\Leftrightarrow5-x-7+2x=0\\ \Leftrightarrow x-2=0\\ \Rightarrow x=2\)
=> Nhận trường hợp này
Vậy x = 2
4)
\(\Leftrightarrow2x+5=5^2=25\\ \Leftrightarrow2x=25-5=20\\ \Rightarrow x=\dfrac{20}{2}=10\)
5)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}-2x+5=0\\ \Leftrightarrow\left|x-2\right|-2x+5=0\)
Nếu \(x\ge2\) thì
\(\Leftrightarrow x-2-2x+5=0\\ \Leftrightarrow3-x=0\\ \Rightarrow x=3\)
=> Nhận trường hợp này
Nếu \(x< 2\) thì
\(\Leftrightarrow2-x-2x+5=0\\ \Leftrightarrow7-3x=0\\ \Leftrightarrow3x=7\\ \Rightarrow x=\dfrac{7}{3}\)
=> Loại trường hợp này
Vậy x = 3
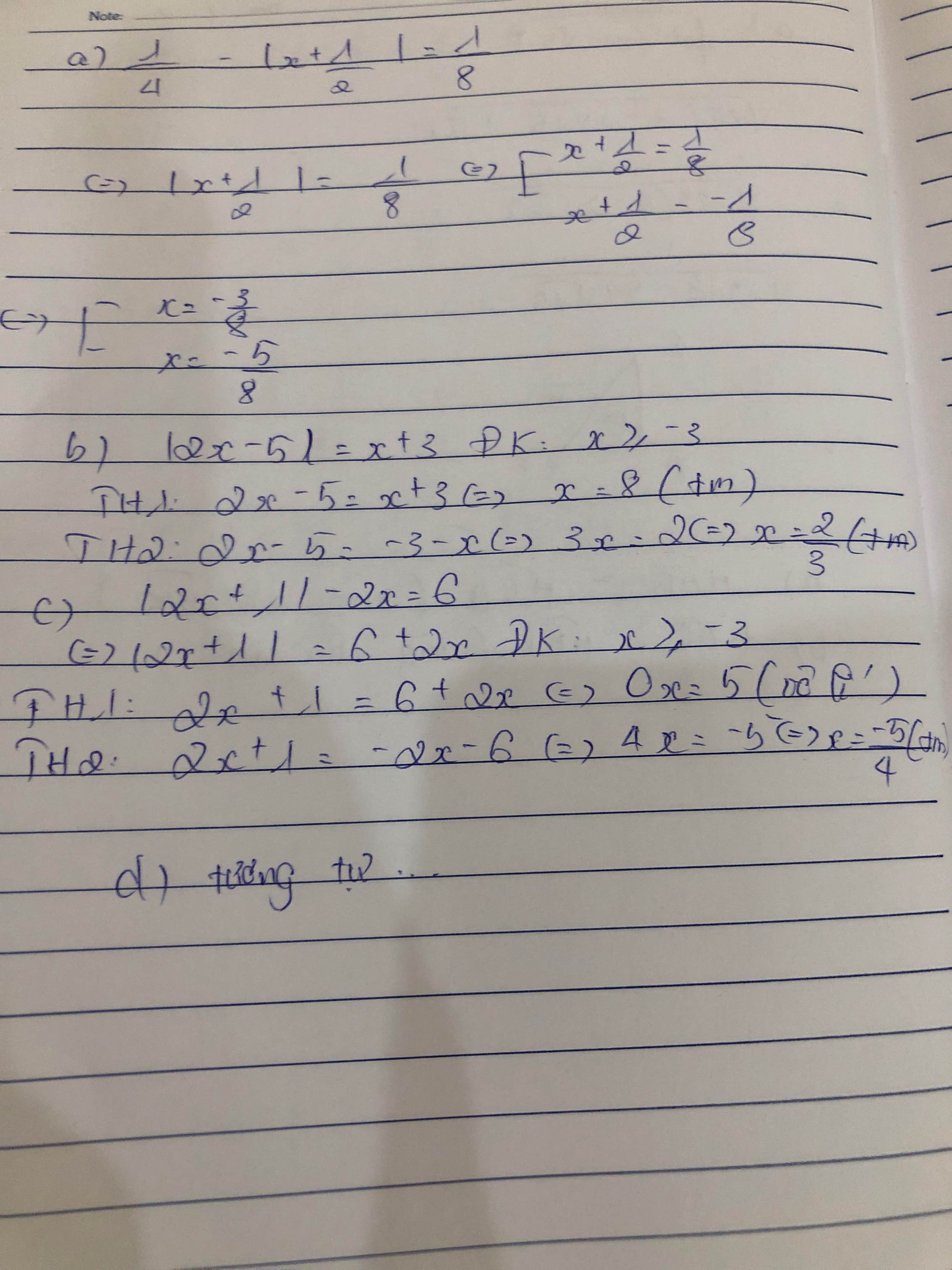
à, mink quen, = 2 chứ, mink vội nên bấm nhầm bạn ạ
2x=4
x=2