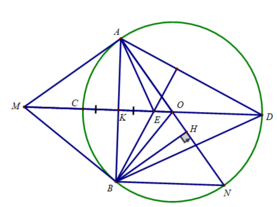
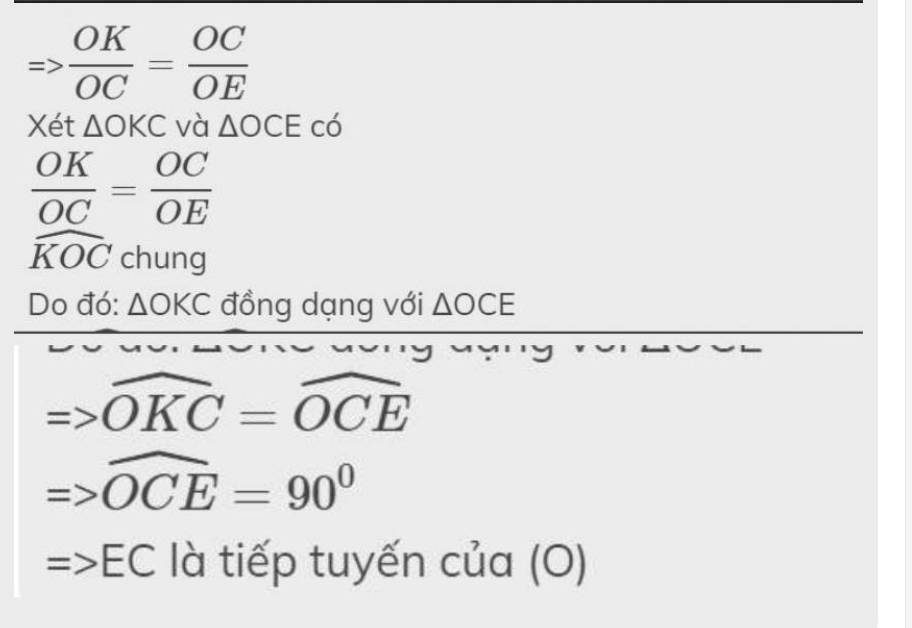
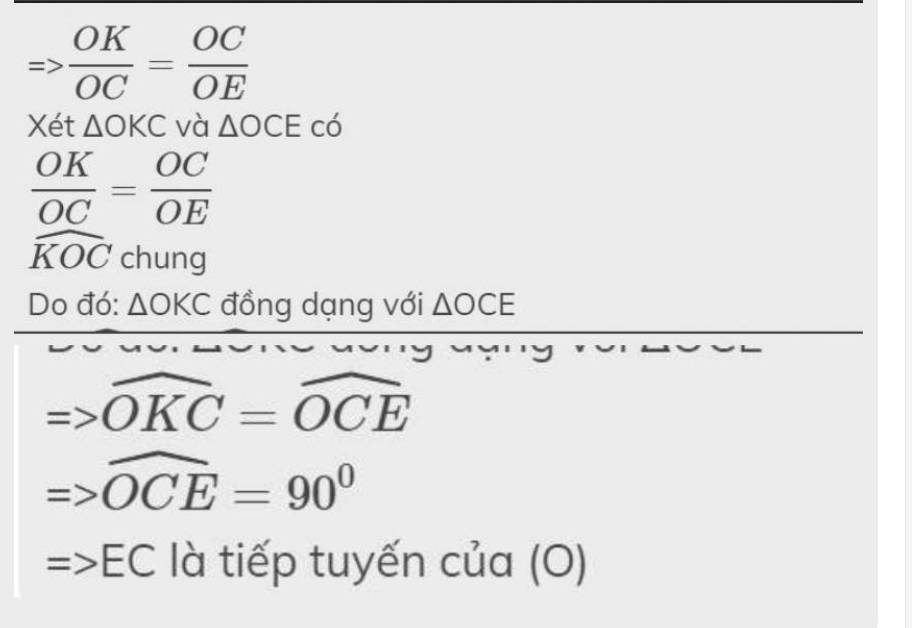
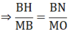Cho đường tròn (O). Từ điểm M ở ngoài đường tròn kẻ 2 tiếp tuyến MA,Mb ( A,B là tiếp điểm). Kẻ AH vuông góc với MB tại H . Đường thẳng AH cắt (O) tại N. đường tròn dường kính NA cắt các đường thẳng AB và MA theo thứ tự tại I và K
a) Chứng minh tứ giác NHBI nội tiếp
b)Chứng minh tam giác NHI đồng dạng với tam giác NIK
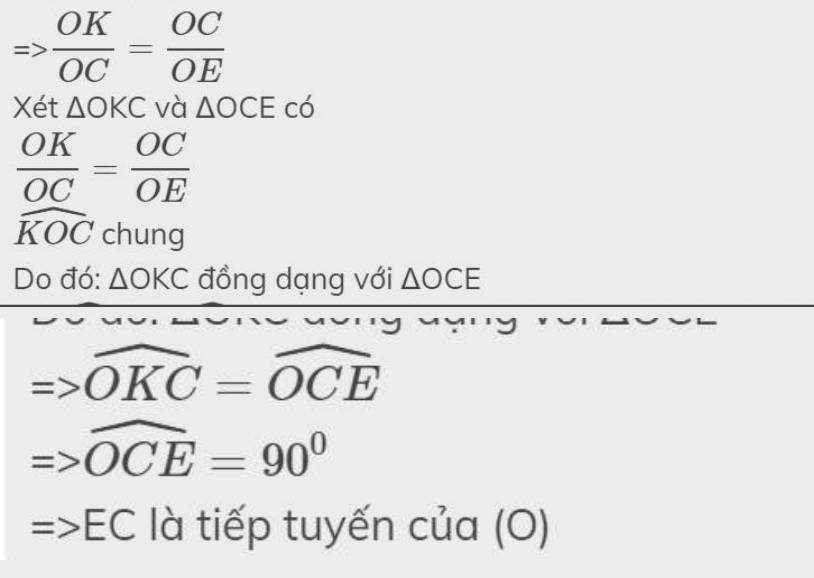
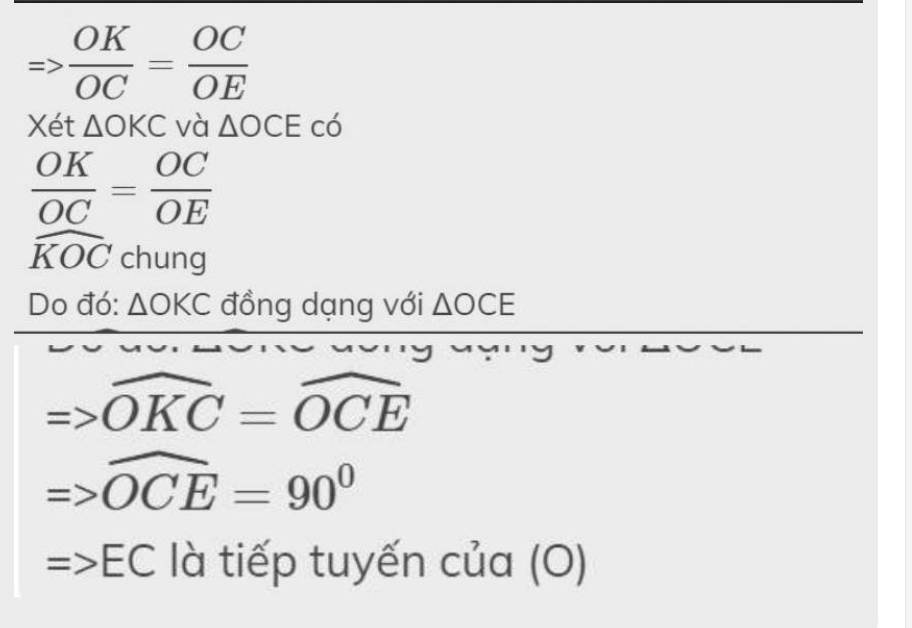
c) Gọi C là giao điểm của NB và HI , gọi D là giao điểm của NA và KI. Đường thẳng CD cắt MA tại E. Chứng minh CI=EA