Cho f(x) =a^2+bx+c . Trong đó 2a+c=0 . Hỏi f(1); f(2) có thể là số dương không? Giúp tớ với, tớ sắp thi rồi🤧
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


f(-1)=a-b+c
f(3)=9a+3b+c
f(3)-f(-1)=8a+b=4(2a+b)
Mà 2a+b=0 =) f(3)-f(-1)=0
=) f(3)=f(-1) =) f(3).f(-1)=(a-b+c)^2
Mà (a-b+c)^2 >= 0 =) f(-1).f(3)>=0
Ta có : f(x) = ax2 + bx + c
=> f( -1 ) = a - b + c
f(3) = 9a + 3b + c
=> f(3) - f( -1 ) = 8a + 4b = 4 ( 2a + b ) = 4.0 = 0
=> f(3) = f( -1 )
=> f( -1 ). f(3) = f(3). f(3) = [ f(3) ]2 \(\ge\) 0
=> đpcm
Study well ! >_<


Có \(c=2a+4b\). Ta tính f ( -1 ) và f ( 2 )
\(f\left(-1\right)=a-b+c=a-b+2a+4b=3a+3b=3\left(a+b\right)\)
\(f\left(2\right)=4a+2b+c=4a+2b+2a+4b=6a+6b=6\left(a+b\right)\)
\(\Rightarrow f\left(-1\right).f\left(2\right)=3\left(a+b\right).6\left(a+b\right)=18\left(a+b\right)^2\)
Có \(\left(a+b\right)^2\ge0\forall x\Leftrightarrow18\left(a+b\right)^2\ge0\forall x\left(đpcm\right)\)

Ta có:
\(f\left(0\right)=c\in Z\)(1)
\(f\left(1\right)=a+b+c\in Z\)(2)
\(f\left(2\right)=4a+2b+c\in Z\)(3)_
Từ (1), (2) => \(a+b\in Z\)=> \(2a+2b\in Z\)(4)
Từ (1), (3)=> 4a+2b\(\in Z\)(5)
Từ (4), (5) => \(\left(4a+2b\right)-\left(2a+2b\right)\in Z\)
=> \(2a\in Z\)=> \(2b\in Z\)

Lời giải:
$f(0)=a.0^2+b.0+c=c$ nguyên
$f(1)=a+b+c$ nguyên, mà $c$ nguyên nên $a+b+c-c=a+b$ nguyên
$f(2)=4a+2b+c=2a+2(a+b)+c$ nguyên mà $a+b, c$ nguyên nên $2a$ nguyên
$2a$ nguyên, $2(a+b)$ nguyên nên $2b$ nguyên.
Ta có đpcm.
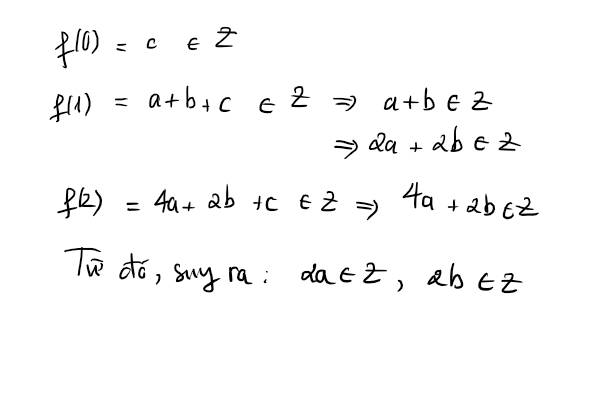
Theo mình hiểu thì $f(x)=ax^2+bx+c$. Thế thì $f(1), f(2)$ hoàn toàn có thể nhận giá trị dương khi $a=-1; c=2; b=2$
Vâng ạ