Cho hình chóp S.ABCD có SA vuông góc với đáy. Đáy ABCD là hình thang vuông ở A, B sao cho AB = BC = AD/2 = a. SA = 2a. a. Xác định góc giữa (SAB) và (SCD). b, Xác định góc giữa (SBD) và (SAB). c. Xác định góc giữa (SBC) và (SCD).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 3 2023
a: (SBD) giao (ABCD)=BD
SO vuông góc BD
AO vuông góc BD
=>((SBD);(ABCD))=góc SOA
b: (SCD) giao (SAD)=SD
Kẻ AH vuông góc SC
ΔSDC vuông tại D
Kẻ DK vuông góc SC
Qua H kẻ HF//DK
=>Góc cần tìm là góc AHF
31 tháng 3 2023
a: (SBD) giao (ABCD)=BD
AB vuông góc BD
SB vuông góc BD
=>góc cần tìm là góc SBA
8 tháng 4 2023
a: \(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ
b:
Kẻ BH vuông góc AC tại H
(SB;SAC)=(SB;SH)=góc BSH
\(HB=\dfrac{a\cdot a}{a\sqrt{2}}=a\cdot\dfrac{\sqrt{2}}{2}\)
AH=AC/2=a*căn 2/2
=>\(SH=\sqrt{a^2+\dfrac{1}{2}a^2}=a\sqrt{\dfrac{3}{2}}\)
\(SH=\dfrac{a\sqrt{6}}{2};HB=\dfrac{a\sqrt{2}}{2};SB=a\sqrt{2}\)
\(cosBSH=\dfrac{SB^2+SH^2-BH^2}{2\cdot SB\cdot SH}=\dfrac{\sqrt{3}}{2}\)
=>góc BSH=30 độ
c: (SD;(SAB))=(SD;SA)=góc ASD
tan ASD=AD/AS=2
nên góc ASD=63 độ
CM
24 tháng 6 2019
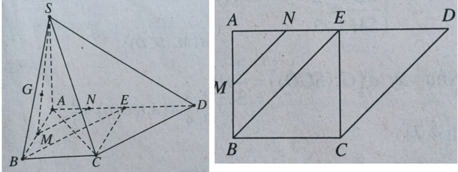
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).
CM
21 tháng 7 2019
a) Ta có:
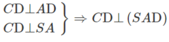
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
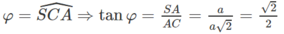
c)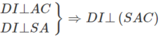 
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và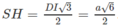 
.
Tam giác SDI có diện tích:
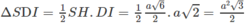
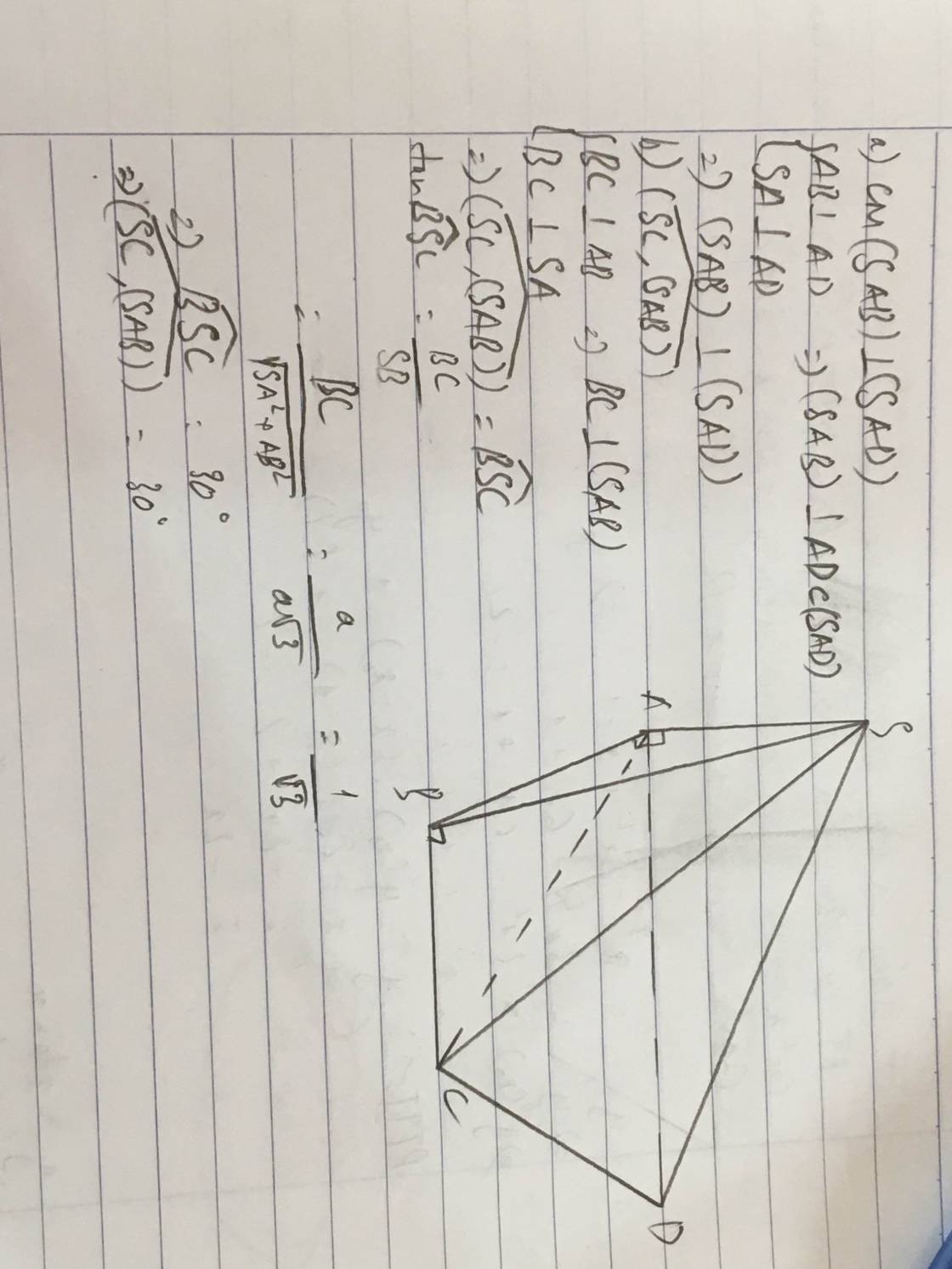
a: Qua S kẻ đường Sx song song SD
=>Sx vuông góc SA
SC vuông góc CD
=>SC vuông góc Sx
((SAB);(SCD))=góc ASC
b: (SBD) căt (SAB)=SB
Kẻ DA vuông góc AB
mà DA vuông góc SA
nên DA vuông góc (SAB)
=>DA vuông góc SB
Kẻ AK vuông góc SB
=>((SBD);(SAB))=góc AKD
c: (SBC) giao (SCD)=SC
Kẻ BH vuông góc SC
Qua H kẻ HF//CD
=>HF vuông góc SC
=>((SBC);(SCD))=góc BHF