Cho MN và PQ cắt nhau tại trung điểm O của mỗi đoạn . chứng minh rằng PM+PQ >2PO
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


HÌNH ẢNH CHỈ MANG TÍNH CHẤT MINH HỌA
a) +) Xét ΔMQO và ΔNPO có
MO = NO ( gt)
\(\widehat{MOQ}=\widehat{NOP}\) ( 2 góc đối đỉnh )
OP = OQ ( gt)
⇒ ΔMQO = ΔNPO ( c-g-c)
b) +) Ta có ΔMQO = ΔNPO ( cmt)
⇒ \(\widehat{OMQ}=\widehat{ONP}\) ( 2 góc tương unsgws )
Mà 2 góc này ở vị trí so le trong
⇒ MQ // NP
@@@ Học tốt
Chiyuki Fujito

a) Xét \(\Delta MOQ\) và \(\Delta NOP\) có:
\(OM=ON\)(O là trung điểm MN)
\(\widehat{MOQ}=\widehat{NOP}\) (đối đỉnh)
\(OP=OQ\) (O là trung điểm PQ)
\(\Rightarrow\Delta MOQ=\Delta NOP\left(c.g.c\right)\)
b) Xét \(\Delta MDO\) và \(\Delta NEO\) có:
\(MD=NE\left(gt\right)\)
\(\widehat{DMO}=\widehat{ONE}\left(\Delta MOQ=\Delta NOP\right)\)
\(OM=ON\) (O là trung điểm MN)
\(\Rightarrow\Delta MDO=\Delta NEO\left(c.g.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}OD=OE\\\widehat{DOM}=\widehat{EON}\end{matrix}\right.\)
Ta có: \(\widehat{DOM}=\widehat{EON}\left(cmt\right)\)
Mà \(\widehat{EON}+\widehat{MOE}=180^0\)(kề bù)
\(\Rightarrow\widehat{DOM}+\widehat{MOE}=180^0\Rightarrow\widehat{DOE}=180^0\)
\(\Rightarrow D,O,E\) thẳng hàng
Mà \(OD=OE\left(cmt\right)\)
=> O là trung điểm DE

a: Xét tứ giác MPNQ có
E là trung điểm của MN
E là trung điểm của QP
Do đó: MPNQ là hình bình hành
Suy ra: MP=NQ
b: Ta có: MPNQ là hình bình hành
nên MQ=NP
c: Ta có: MPNQ là hình bình hành
nên MP//NQ

mình không vẽ hình được, sorry bạn nhé
ΔMPO và ΔQNO có
O1=O2 (đối đỉnh)
MO= OQ (gt)
PO= QN (gt)
⇒ ΔMOP= ΔQNO (c.g.c)
⇒ MP= QN (hai cạnh tương ứng)
ΔMQO vàΔPNO có
MO= OQ (gt)
PO= QN (gt)
O3= O4 (đối đỉnh)
⇒ΔMQO=ΔPNO(c.g.c)
⇒MQ=PN(2 cạnh tương ứng)

a: Đề thiếu rồi bạn
b: Xét tứ giác MQNP có
Olà trung điểm của MN
O là trung điểm của QP
Do đó: MQNP là hình bình hành
Suy ra: MQ//NP

b: Xét tứ giác MPNQ có
O là trung điểm của MN
O là trung điểm của PQ
Do đó: MPNQ là hình bình hành
Suy ra MQ//PN

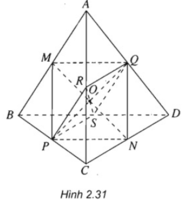
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.


PM>0
=>PM+PQ>PQ
=>PM+PQ>2PO