cho tam giác ABC vuông tại đỉnh A, A(-1;4), B(1;-4) và đường thẳng BC đi qua điểm M\(\left(2;\dfrac{1}{2}\right)\). xác định tọa độ đỉnh C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ΔABCΔABC có : ˆA+ˆABC+ˆB=1800A^+ABC^+C^=1800 ( tổng ba góc của một tam giác )
⇒900+ˆABC+700=1800⇒600+ABC^+700=1800
⇒ˆABC=1800−(700+900)=200⇒ABC^=1800−(700+600)=500
Mà ˆABC+ˆABD=1800ABC^+ABD^=1800 ( hai góc kề bù )
⇒200+ˆABD=1800⇒500+ABD^=1800

a) Tam giác ABC nhọn:
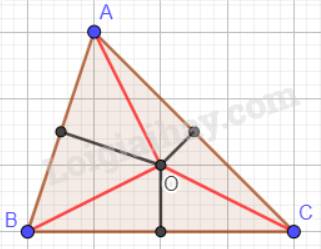
b) Tam giác ABC vuông tại A:
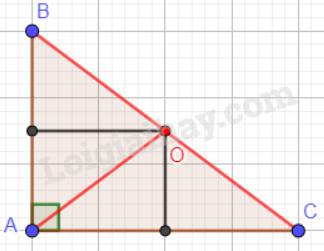
c) Tam giác ABC có góc A tù:
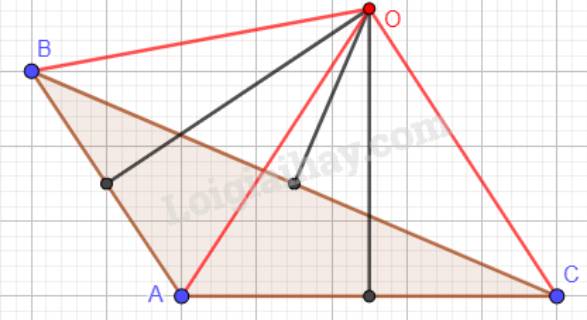

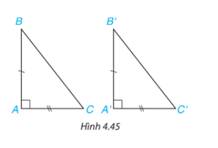
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)

\(\Delta ABC\perp A\) \(\Rightarrow\widehat{B}+\widehat{C}=90^0\)
= > Góc B và Góc C phải là 2 góc nhọn
Góc ngoài đỉnh B = \(180^0-\widehat{B}\)mà Góc B nhọn = > Góc ngoài tại đỉnh B là góc tù

Kẻ \(AH\perp BC\) tại H
Áp dụng hệ thức lượng trong tam giác vuông BAC có:
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
Do AD và AE lần lượt là hai tia phân giác trong và ngoài tại đỉnh A
\(\Rightarrow AD\perp AE\)
Áp dụng hệ thức lượng vào tam giác vuông AED có:
\(\dfrac{1}{AE^2}+\dfrac{1}{AD^2}=\dfrac{1}{AH^2}\) (AH là đường cao của tam giác AED do \(AH\perp BC\) hay \(AH\perp ED\))
\(\Rightarrow\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AE^2}+\dfrac{1}{DA^2}\)
Vậy...
\(\overrightarrow{BM}=\left(1;\dfrac{9}{2}\right)\)
vecto BC=(x-1;y+4)
vecto AC=(x+1;y-4)
vecto AB=(2;-8)
Theo đề, ta có: 1/x-1=9/2(y+4) và 2(x+1)-8(y-4)=0
=>9(x-1)=2(y+4) và 2x+2-8y+32=0
=>9x-9-2y-8=0 và 2x-8y=-34
=>x=3 và y=5
=>C(3;5)