Giải PT: 1/(2019x+1) + 1/(2022x+5) = 1/(2021x+4) + 1/(2022x+2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
1
24 tháng 10 2021
\(a,Sửa:2021x-1+2022x\left(1-2021x\right)=0\\ \Leftrightarrow\left(2021x-1\right)\left(1-2022x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2021}\\x=\dfrac{1}{2022}\end{matrix}\right.\)
2 tháng 12 2021
\(1,\left(x+2022\right)\left(x-1\right)=x^2+2021x-2022\left(B\right)\\ 2,\left(a+b\right)\left(a^2-ab+b^2\right)=a^3+b^3\left(A\right)\)
KD
1
9 tháng 2 2021
ĐKXĐ: \(x\notin\left\{-\dfrac{1}{2018};-\dfrac{2}{2019};-\dfrac{1}{505};\dfrac{-5}{2021}\right\}\)
Ta có: \(\dfrac{1}{2018x+1}-\dfrac{1}{2019x+2}=\dfrac{1}{2020x+4}-\dfrac{1}{2021x+5}\)
\(\Leftrightarrow\dfrac{2019x+2-2018x-1}{\left(2018x+1\right)\left(2019x+2\right)}=\dfrac{2021x+5-2020x-4}{\left(2020x+4\right)\left(2021x+5\right)}\)
\(\Leftrightarrow\dfrac{x+1}{\left(2018x+1\right)\left(2019x+2\right)}=\dfrac{x+1}{\left(2020x+4\right)\left(2021x+5\right)}\)
\(\Leftrightarrow\dfrac{x+1}{\left(2018x+1\right)\left(2019x+2\right)}-\dfrac{x+1}{\left(2020x+4\right)\left(2021x+5\right)}=0\)
\(\Leftrightarrow\left(x+1\right)\left(\dfrac{1}{\left(2018x+1\right)\left(2019x+2\right)}-\dfrac{1}{\left(2020x+4\right)\left(2021x+5\right)}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\\dfrac{1}{\left(2018x+1\right)\left(2019x+2\right)}=\dfrac{1}{\left(2020x+4\right)\left(2021x+5\right)}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\\left(2018x+1\right)\left(2019x+2\right)=\left(2020x+4\right)\left(2021x+5\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\4074342x^2+6055x+2=4082420x^2+18184x+20\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(nhận\right)\\-8078x^2-12129x-18=0\end{matrix}\right.\)
Ta có: \(-8078x^2-12129x-18=0\)(2)
\(\Delta=\left(-12129\right)^2-4\cdot\left(-8078\right)\cdot\left(-18\right)=146531025\)
Vì \(\Delta>0\) nên phương trình (2) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{12129-12105}{2\cdot\left(-8078\right)}=\dfrac{-6}{4039}\left(nhận\right)\\x_2=\dfrac{12129+12105}{2\cdot\left(-8078\right)}=-\dfrac{3}{2}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{-1;\dfrac{-6}{4039};\dfrac{-3}{2}\right\}\)
H9
HT.Phong (9A5)
CTVHS
3 tháng 9 2023
a) \(\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{90}\right)\cdot100-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{9\cdot10}\right)\cdot100-\left[\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\left(1-\dfrac{1}{2}+\dfrac{1}{2}-...+\dfrac{1}{9}-\dfrac{1}{10}\right)\cdot100-\left[\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\left(1-\dfrac{1}{10}\right)\cdot100-\left[\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\dfrac{9}{10}\cdot100-\left[\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow90-\left[\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)=90-89\)
\(\Rightarrow\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)=1\)
\(\Rightarrow x+\dfrac{103}{50}=\dfrac{5}{2}\)
\(\Rightarrow x=\dfrac{11}{25}\)
b) \(x\cdot9,85+x\cdot0,15=0,1\)
\(\Rightarrow x\cdot\left(9,85+0,15\right)=0,1\)
\(\Rightarrow x\cdot10=0,1\)
\(\Rightarrow x=\dfrac{0,1}{10}\)
\(\Rightarrow x=0,01\)
c) \(\dfrac{2}{5}+2022x=\dfrac{4}{10}\)
\(\Rightarrow\dfrac{2}{5}+2022x=\dfrac{2}{5}\)
\(\Rightarrow2022x=\dfrac{2}{5}-\dfrac{2}{5}\)
\(\Rightarrow2022x=0\)
\(\Rightarrow x=\dfrac{0}{2022}\)
\(\Rightarrow x=0\)
3 tháng 9 2023
a) \(\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{90}\right).100-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\left(1\right)\)
Ta có :
\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{90}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=1-\dfrac{1}{10}=\dfrac{9}{10}\)
\(\left(1\right)\Rightarrow\dfrac{9}{10}.100-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow90-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right].2=89\)
\(\Rightarrow\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right].2=90-89\)
\(\Rightarrow\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)=\dfrac{1}{2}\)
\(\Rightarrow x+\dfrac{206}{100}=\dfrac{5}{2}:\dfrac{1}{2}\)
\(\Rightarrow x+\dfrac{103}{50}=\dfrac{5}{2}.\dfrac{2}{1}\)
\(\Rightarrow x+\dfrac{103}{50}=5\)
\(\Rightarrow x=5-\dfrac{103}{50}\)
\(\Rightarrow x=\dfrac{250}{50}-\dfrac{103}{50}\)
\(\Rightarrow x=\dfrac{147}{50}\)
NG
1
20 tháng 10 2023
a: \(2022^{x-2021}+3=\left(7-5\right)^2\)
=>\(2022^{x-2021}+3=4\)
=>\(2022^{x-2021}=1\)
=>x-2021=0
=>x=2021
b: \(\left(x+1\right)+\left(x+2\right)+...+\left(x+30\right)=795\)
=>\(30x+\left(1+2+3+...+30\right)=795\)
=>\(30x+\dfrac{30\cdot31}{2}=795\)
=>\(30x=795-31\cdot15=330\)
=>x=11
KH
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt[3]{x+1}\left(\sqrt[]{2022x^2+x+1}-1\right)+\sqrt[3]{x+1}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{\sqrt[3]{x+1}.\left(2022x^2+x\right)}{\sqrt[]{2022x^2+x+1}+1}+\dfrac{x}{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{\sqrt[3]{x+1}\left(2022x+1\right)}{\sqrt[]{2022x^2+x+1}+1}+\dfrac{1}{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}\right)\)
\(=\dfrac{1}{1+1}+\dfrac{1}{1+1+1}=\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}\)
NB
1
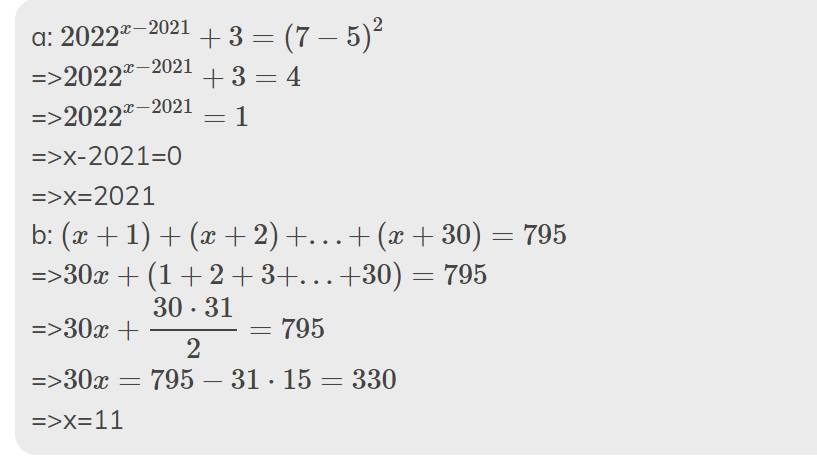
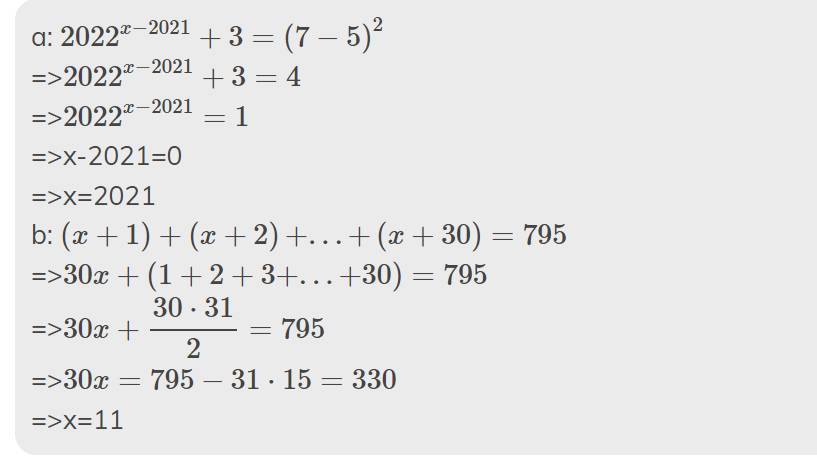
pls help me