Cho Parabol y=1/4x2 . Xác định m để A(4; m) nằm trên parabol.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thay x = 2 ; y = m vào hàm số y = 1 4 x 2
ta được m = 1 4 . 2 2 = 1 2
Vậy m = 1 2
Đáp án cần chọn là: A

Thay x = m 5 ; y = −2 5 vào hàm số y = − 5 x 2 ta được
− 2 5 = − 5 . m 5 2 ⇔ − 5 m 5 = 2 5 ⇔ m = − 2 5
Vậy m = − 2 5
Đáp án cần chọn là: D

Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{4}x^2-mx-n=0\)
THeo đề, ta có:
\(\left\{{}\begin{matrix}m+n=2\\\left(-m\right)^2-4\cdot\left(-\dfrac{1}{4}\right)\cdot\left(-n\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2-n\\m^2-n=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2-n\\n^2-4n+4-n=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n\in\left\{1;4\right\}\\m\in\left\{1;-2\right\}\end{matrix}\right.\)

parabol (P): y = x 2 ; đường thẳng (d): y = 2x + m (m là tham số).
a) phương trình hoành độ giao điểm của (P) và (d) là:
x 2 = 2x + m ⇔ x 2 - 2x - m = 0
Δ'= 1 + m
(d) tiếp xúc với (P) khi phương trình hoành độ giao điểm có duy nhất 1 nghiệm
⇔ Δ'= 1 + m = 0 ⇔ m = -1
Khi đó hoành độ giao điểm là x = 1

a:
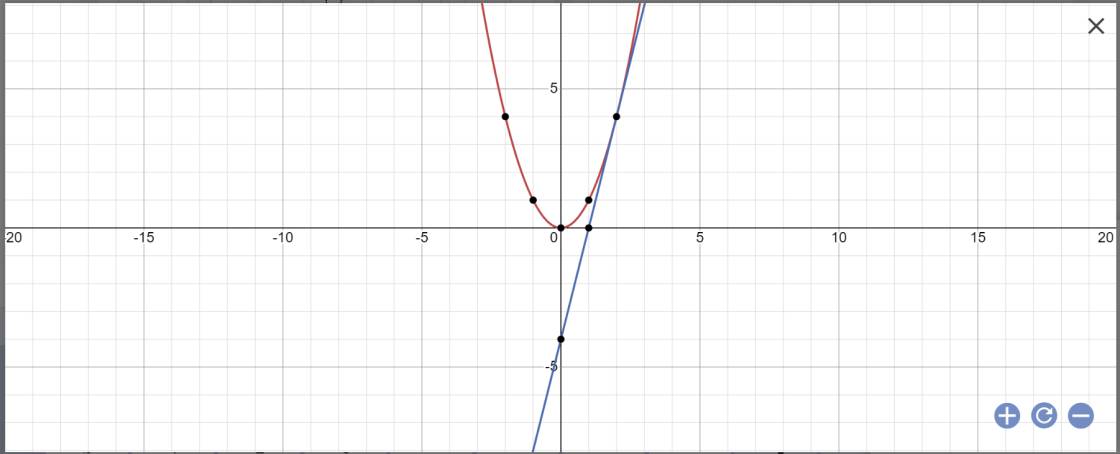
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1

Đường thẳng y = mx + n đi qua điểm A ( -1 ; -2 ) nên
-2 = -m + n ,suy ra n = m-2
Phương trình đường thẳng có dạng y = mx + ( m -2 ) .Điều kiện để đường thẳng tiếp xúc với parabol là phương trình \(\frac{x^2}{4}=mx+\left(m-2\right)\) (1)
có nghiệm kép .Biến đổi (1) ta được : x2 -4.m.x - 4. ( m-2) =0 (2)
Điều kiện để ( 1 ) cũng có nghĩa là ( 2 ) có nghiệm kép là :
\(\Delta'=4m^2+4m-8=0\Leftrightarrow m^2+m-2=0\)
<=> ( m+2 ) . ( m-1 ) = 0 <=> m =-2 hoặc m = 1 .
Vậy các hệ số m , ncaanf tìm là m = -2 ; n = -4 và m =1 ; n=-1

a, Thay m = -1/2 vào (d) ta được :
\(y=2x-2.\left(-\frac{1}{2}\right)+2\Rightarrow y=2x+3\)
Hoành độ giao điểm thỏa mãn phương trình
\(2x+3=x^2\Leftrightarrow x^2-2x-3=0\)
\(\Delta=4-4\left(-3\right)=4+12=16>0\)
\(x_1=\frac{2-4}{2}=-1;x_2=\frac{2+4}{2}=3\)
Vói x = -1 thì \(y=-2+3=1\)
Vớ x = 3 thì \(y=6+3=9\)
Vậy tọa độ giao điểm của 2 điểm là A ( -1 ; 1 ) ; B ( 3 ; 9 )
b, mình chưa học
\(y_1+y_2=4\left(x_1+x_2\right)\)
\(\Leftrightarrow x_1^2+x_2^2=4\left(x_1+x_2\right)\)(1)
Xét phương trình hoành độ giao điểm của (d) và (P) ta có:
\(x^2=2x-2m+2\)
\(\Leftrightarrow x^2-2x+2m-2=0\)
Theo hệ thức Vi-et ta có:
\(\hept{\begin{cases}x_1+x_2=2\\x_1x_2=2m-2\end{cases}}\)
Từ (1) \(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\left(x_1+x_2\right)\)
\(\Leftrightarrow4-4m+4=8\)
\(\Leftrightarrow m=0\)
vậy..

a: Thay x=2 vào (P),ta được:
y=2^2/2=2
2: Thay x=2 và y=2 vào (d), ta được:
m-1+2=2
=>m-1=0
=>m=1
Do A nằm trên parabol thay tọa độ A vào pt parabol ra được:
\(\dfrac{1}{4}.4^2=m\)
\(\Rightarrow m=4\)