hai xe máy xuất phát từ 2 thị trấn A và B cùng một lúc và đi ngược chiêu nhau . Xe từ A đi vs vận tốc hơn xe từ B là 4km/h .hai xe cùng khởi hành lúc 6h30 phút đến 7h15 phút thì gặp nhau . hỏi mỗi xe đi vs vận tốc bằng bao nhiêu ? bt 2 thị trấn A và B cách nhau 60km
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Thời gian hai xe gặp nhau là:
7 giờ 15 phút - 6 giờ 30 phút = 45 phút
45 phút = giờ
Tổng vận tốc hai xe là:
60 : = 80 (km/h)
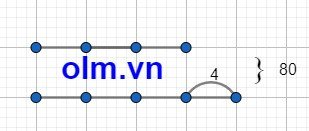
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Vận tốc của xe đi từ A là: (80 + 4): 2 = 42 (km/h)
Vận tốc của xe đi từ B là: 42 - 4 = 38 (km/h)
Đáp số:...

Giải:
Thời gian hai xe gặp nhau là:
7 giờ 15 phút - 6 giờ 30 phút = 45 phút
45 phút = \(\dfrac{3}{4}\) giờ
Tổng vận tốc hai xe là:
60 : \(\dfrac{3}{4}\) = 80 (km/h)
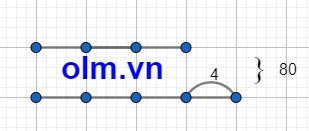
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Vận tốc của xe đi từ A là: (80 + 4): 2 = 42 (km/h)
Vận tốc của xe đi từ B là: 42 - 4 = 38 (km/h)
Đáp số:...

Giải:
Thời gian hai xe gặp nhau là:
7 giờ 15 phút - 6 giờ 30 phút = 45 phút
45 phút = \(\dfrac{3}{4}\) giờ
Tổng vận tốc hai xe là:
60 : \(\dfrac{3}{4}\) = 80 (km/h)
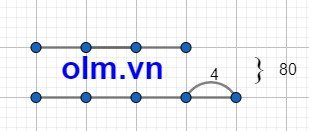
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Vận tốc của xe đi từ A là: (80 + 4): 2 = 42 (km/h)
Vận tốc của xe đi từ B là: 42 - 4 = 38 (km/h)
Đáp số:...

Gọi thời gian dự định đi từ A đến B là x ( giờ) ( x>0)
=> quãng đường AB : 12x
1h20'=1/3=4/3h
Theo bài ra, ta có pt:
\(\frac{1}{3}.\frac{12x}{2}+\frac{20}{60}+\frac{2}{3}.\frac{12x}{36}=x-\frac{4}{3}\)
giải ra được \(x=\frac{15}{4}\) (giờ)
Vậy độ dài quãng đường AB : 12.\(\frac{15}{4}=45\left(km\right)\)
gọi vận tốc xe chậm và nhanh là x,y (km/h) với x,y>0
→độ dài AB:5x+5y=400
nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
→thời gian xe chậm đi là :5h22p=161/30h
Thời gian xe nhanh đi:5h22p -40p =4h42p =47/10h
→Độ dài AB :161/30x +47/10y=400
Theo bài ra ta có hệ: 5x+5y=400 và 161/30x +47/10y=400
→ x+y=80 và 161x+141y=12000
Vậy : x=36 ,y=44 (km/h)

Lời giải:
Đổi 40' = $\frac{2}{3}$ giờ
Gọi vận tốc xe nhanh là a và xe chậm là b (đơn vị: km/h)
Theo bài ra ta có:
$a+b=400:5=80(1)$
Kể từ khi xe nhanh xuất phát, hai xe đi ngược chiều nhau 1 quãng đường có độ dài $400-\frac{2}{3}b$ (km). Hai xe gặp nhau sau $5h22'=\frac{161}{30}$ giờ. Khi đó ta có:
$a+b=(400-\frac{2}{3}b):\frac{161}{30}(2)$
Từ $(1); (2)\Rightarrow (400-\frac{2}{3}b): \frac{161}{30}=80$
$\Rightarrow b=-44$ (km) (vô lý)

Gọi vận tốc ô tô khởi hành từ tỉnh A là x (km/h)
Gọi vận tốc ô tô khởi hành từ tỉnh B là y (km/h)
(ĐK: \(x>y>0\) )
Đổi: \(5h22'=\dfrac{161}{30}h,40'=\dfrac{2}{3}h\)
Hai ô tô đi ngược chiều và gặp nhau sau 5h nên ta có phương trình:
\(5x+5y=400\)
Quãng đường ô tô từ tỉnh A đi được đến lúc gặp nhau là: \(\dfrac{161}{30}x\left(km\right)\)
Quãng đường ô tô từ tỉnh B đi được đến lúc gặp nhau là: \(\dfrac{161}{30}y-\dfrac{2}{3}y=\dfrac{47}{10}y\left(km\right)\)
Do đó ta có phương trình:
\(\dfrac{161}{30}x+\dfrac{47}{10}y=400\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{161}{30}x+\dfrac{47}{10}y=400\\5x+5y=400\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=36\\y=44\end{matrix}\right.\)
Vậy vận tốc ô tô khởi hành từ tỉnh A là 36 (km/h)
Vận tốc ô tô khởi hành từ tỉnh B là 44 (km/h).
van toc xe A:42
van toc xe B:38
nho k cho toi nhe
VẬN TỐC CỦA XE A LÀ 42 KM/H
VẬN TỐC CỦA XE B LÀ 38 KM/H
ĐÂY LÀ 2 ĐÁP ÁN ĐÚNG NHẤT ĐÓ
ĐÚNG 100% NHA,!)))))