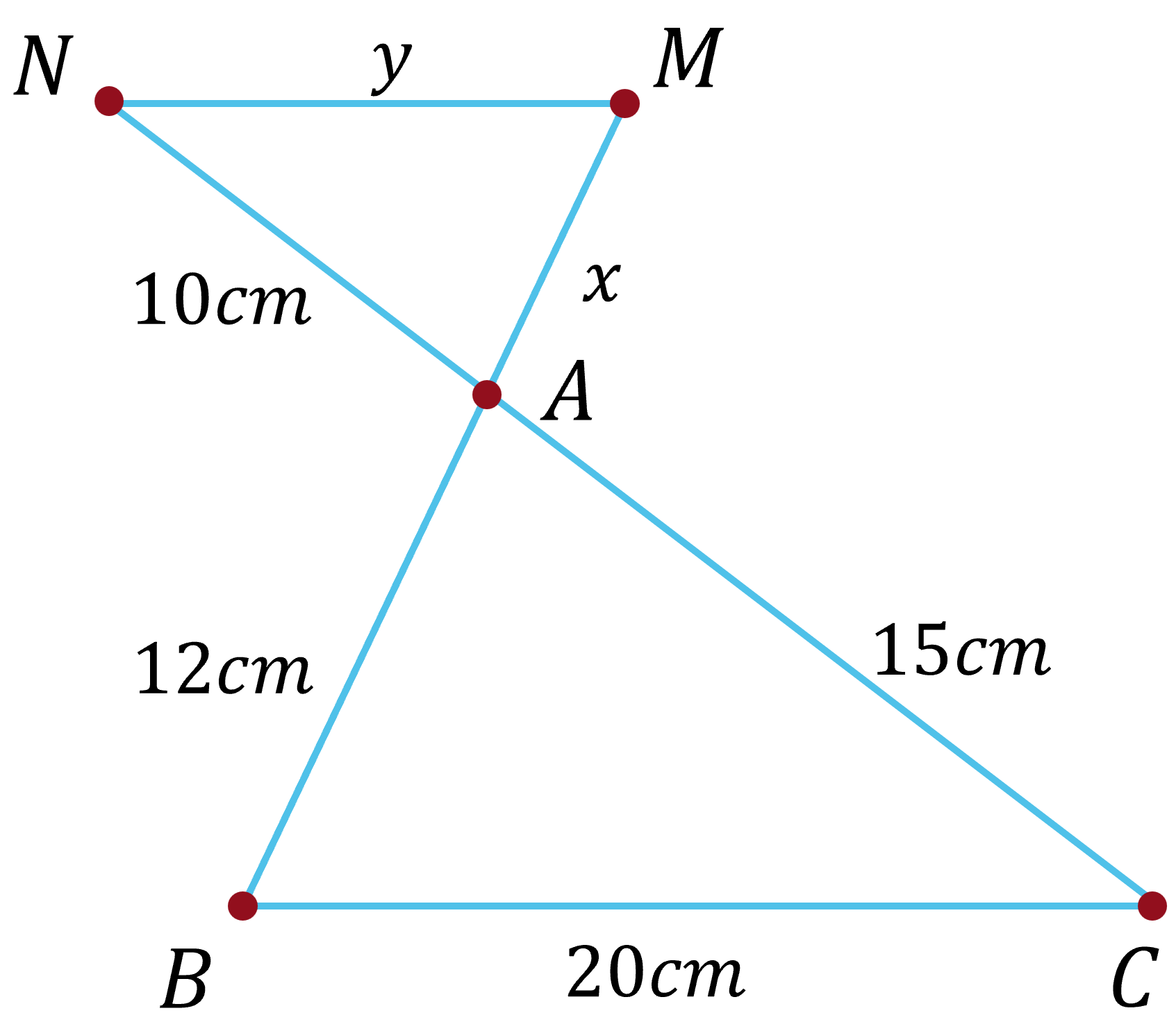
(1,5 điểm) Cho hình vẽ, biết $MN \parallel BC$. Tìm $x$, $y$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: MN//BC ⇒ AM/ AB = AN/AC ⇔ 2/5 = 1,5/x ⇒ x = 3.75
Chọn đáp án C.

Ta có: MN//BC ⇒ AM/AB = AN/AC ⇔ 2/5 = 1,5/x ⇒ x = 5.1,5/2 = 3,75
Chọn đáp án C.

Ta có: MN // BC (gt), áp dụng hệ quả của định lý Ta – lét suy ra:
Suy ra: 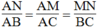 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
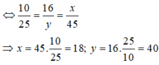

Trong ΔABC, ta có: MN // BC (gt)
Suy ra: 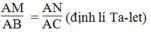
Suy ra: 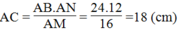
Vậy NC = AC – AN = 18 – 12 = 6(cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
M N 2 = A M 2 + A N 2 = 16 2 + 12 2 = 400
MN = 20cm
Trong ΔABC, ta có: MN // BC (gt)
Suy ra:![]()
Vậy: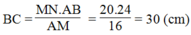

Xét tam giác OAB có \(\frac{{OM}}{{MA}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Xét tam giác OBC có \(\frac{{OP}}{{PC}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Từ đó ta có \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}}\).
Xét tam giác OAC với \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}} \Rightarrow MP\parallel AC\) (Hệ quả của định lý Thales).

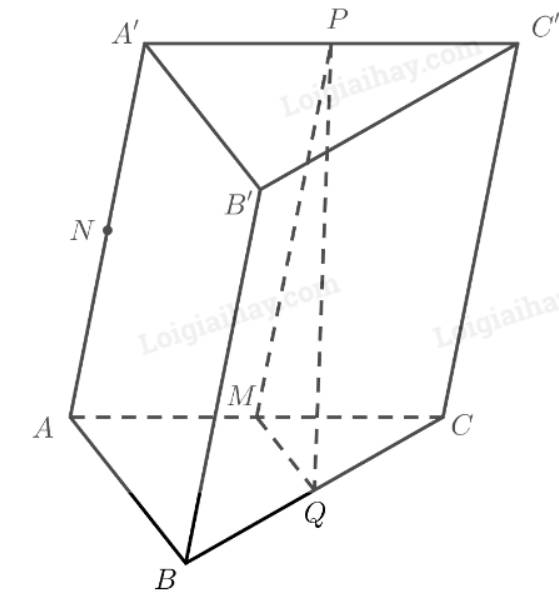
Ta có: \(M\) là trung điểm của \(AC\)
\(Q\) là trung điểm của \(BC\)
\( \Rightarrow MQ\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow MQ\parallel AB\\AB \subset \left( {ABA'} \right)\end{array} \right\} \Rightarrow MQ\parallel \left( {ABA'} \right)\)
\(M\) là trung điểm của \(AC\)
\(P\) là trung điểm của \(A'C'\)
\( \Rightarrow MP\) là đường trung bình của hình bình hành \(ACC'A'\)
\(\left. \begin{array}{l} \Rightarrow MP\parallel AA'\\AA' \subset \left( {ABA'} \right)\end{array} \right\} \Rightarrow MP\parallel \left( {ABA'} \right)\)
\(\left. \begin{array}{l}MQ\parallel \left( {ABA'} \right)\\MP\parallel \left( {ABA'} \right)\\MP,MQ \subset \left( {MPQ} \right)\end{array} \right\} \Rightarrow \left( {MPQ} \right)\parallel \left( {ABA'} \right)\)
Chọn D.
Vì MN // BC theo Talet ta có:
\(\dfrac{y}{20}\) = \(\dfrac{10}{15}\) = \(\dfrac{x}{12}\) => x = \(\dfrac{10}{15}\) . 12 = 8; y = \(\dfrac{10}{15}\) . 20 = \(\dfrac{40}{3}\)