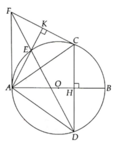
Cho đường tròn (O) đường kính AB cố định, điểm H nằm giữa hai điểm A và O. Kẻ dây CD vuông góc với AB tại H. Lấy điểm F thuộc cung AC nhỏ, BF cắt CD tại E, AF cắt DC tại I.
a) CMR: tứ giác AHEF là tứ giác nội tiếp.
b) CMR: góc BFH = góc EAB, từ đó ⇒ BE.BF=BH.BA.
c) Đường tròn ngoại tiếp ΔIEF cắt AE tại điểm thứ hai M. CMR: ΔHIA ~ ΔHBE và điểm M thuộc (O)
d) Tìm vị trí của H trên OA để ΔOHD có chu vi lớn nhất