Cho A và B là 2 điểm khác nhau ,nằm trong nửa mp bờ xy, C là điểm đối xứng với A qua đường thẳng xy. Đường thẳng xy cắt BC tại D
CMR: Nếu điểm E thuộc xy ( E khác D) ta có AE+BE>AD+BD
mìn cần gấp
ai đúng mình tk cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 12 2019
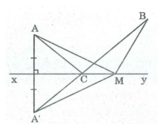
Vì A' đối xứng với A qua xy
⇒ xy là đường trung trực của AA'.
⇒ CA' = CA (t/chất đường trung trực)
MA' = MA (t/chất đường trung trực)
AC + CB = A'C + CB = A'B (1)
MA + MB = MA'+ MB (2)
Trong ∆ MA'B, ta có:
A'B < A'M + MB (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB
P
5 tháng 1 2018
Câu 2
Kẻ D doi xung voi A qua Ox
E doi xung voi A qua Oy
Goi B' la 1 diem bat ki tren Ox,C' la 1 diem bat ki tren Oy
Do Ox la duong trung truc cua AD
=> BA=BD,B'A=B'A
Tuong tu=> C'A=C'E,CA=CE
Ta co
PABC=AB+BC+AC
Ma AB=BD.AC=CE
=>PABC=BC+BD+CE=ED
lai co B'D+B'E\(\ge ED\)
B'C'\(\ge B'E\)
=> B'D+B'C'+C'E\(\ge ED\)
=>PAB'C'\(\ge P_{ABC}\)
Dau ''='' xay ra khi B'\(\equiv B,C'\equiv C\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
10 tháng 1 2017
+ Ta có AB vuông góc với AC và CD vuông góc với AC => AB//CD (cùng vuông góc với AC) (1)
+ Xét tg ABC và tg ACE có
BC=AE
AC chung
BC//AE => ^ACB=^CAE (góc so le trong)
=> tg ABC = tg ACE => ^BAC=^ACE=90 => CE//AB (có 2 góc so le trong bằng nhau) (2)
Từ (1) và (2) => CD trùng CE (qua 1 điểm (điểm C) chỉ dựng được duy nhất 1 đường thẳng // với 1 đường thẳng khác)
=> D; C; E thẳng hàng
trong sách giáo khóa cũng có