Giải hệ phương trình x3+4y=y3+16x và 1+y2=5(1+x2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x 3 + 4 y = y 3 + 16 x 1 + y 2 = 5 ( 1 + x 2 ) ( 1 )
– Xét x = 0, hệ (I) trở thành 4 y = y 3 y 2 = 4 < = > y = ± 2
– Xét x ≠ 0, đặt y x = t < = > y = x t . Hệ (I) trở thành
x 3 + 4 x t = x 3 t 3 + 16 x 1 + x 2 t 2 = 5 ( 1 + x 2 ) < = > x 3 ( t 3 − 1 ) = 4 x t − 16 x x 2 ( t 2 − 5 ) = 4 < = > x 3 ( t 3 − 1 ) = 4 x ( t − 4 ) ( 1 ) 4 = x 2 ( t 2 − 5 ) ( 2 )
Nhân từng vế của (1) và (2), ta được phương trình hệ quả
4 x 3 ( t 3 − 1 ) = 4 x 3 ( t − 4 ) ( t 2 − 5 ) < = > t 3 − 1 = t 3 − 4 t 2 − 5 t + 20 (Do x ≠ 0) <=>4t 2 + 5 t − 21 = 0 < = > t = − 3 t = 7 4
+ Với t = – 3, thay vào (2) được x2 = 1 ⇔ x = ±1.
x = 1 thì y = –3, thử lại (1;–3) là một nghiệm của (I)
x = –1 thì y = 3, thử lại (–1;3) là một nghiệm của (I)
+ Với t = 7/4 , thay vào (2) được x 2 = − 64 31 (loại)
Vậy hệ (I) có các nghiệm (0;2), (0;–2), (1;–3), (–1;3).

10: \(x\left(x-y\right)+x^2-y^2\)
\(=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x+x+y\right)\)
\(=\left(x-y\right)\left(2x+y\right)\)
11: \(x^2-y^2+10x-10y\)
\(=\left(x^2-y^2\right)+\left(10x-10y\right)\)
\(=\left(x-y\right)\left(x+y\right)+10\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y+10\right)\)
12: \(x^2-y^2+20x+20y\)
\(=\left(x^2-y^2\right)+\left(20x+20y\right)\)
\(=\left(x-y\right)\left(x+y\right)+20\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y+20\right)\)
13: \(4x^2-9y^2-4x-6y\)
\(=\left(4x^2-9y^2\right)-\left(4x+6y\right)\)
\(=\left(2x-3y\right)\left(2x+3y\right)-2\left(2x+3y\right)\)
\(=\left(2x+3y\right)\left(2x-3y-2\right)\)
14: \(x^3-y^3+7x^2-7y^2\)
\(=\left(x^3-y^3\right)+\left(7x^2-7y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\cdot\left(x^2-y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+7x+7y\right)\)
15: \(x^3+4x-\left(y^3+4y\right)\)
\(=x^3-y^3+4x-4y\)
\(=\left(x^3-y^3\right)+\left(4x-4y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+4\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+4\right)\)
16: \(x^3+y^3+2x+2y\)
\(=\left(x^3+y^3\right)+\left(2x+2y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+2\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2+2\right)\)
17: \(x^3-y^3-2x^2y+2xy^2\)
\(=\left(x^3-y^3\right)-\left(2x^2y-2xy^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-2xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-2xy\right)\)
\(=\left(x-y\right)\left(x^2-xy+y^2\right)\)
18: \(x^3-4x^2+4x-xy^2\)
\(=x\left(x^2-4x+4-y^2\right)\)
\(=x\left[\left(x^2-4x+4\right)-y^2\right]\)
\(=x\left[\left(x-2\right)^2-y^2\right]\)
\(=x\left(x-2-y\right)\left(x-2+y\right)\)

từ phương trình số 2 ta có
\(\left(x+y\right)\left(x+2y\right)+\left(x+y\right)=0\Leftrightarrow\left(x+y\right)\left(x+2y+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+y=0\\x+2y+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-y\\x=-2y-1\end{cases}}\)
lần lượt thay vào 1 ta có
\(\orbr{\begin{cases}y^2+7=y^2+4y\\\left(-2y-1\right)^2+7=y^2+4y\end{cases}\Leftrightarrow\orbr{\begin{cases}y=\frac{7}{4}\\3y^2+8=0\end{cases}}}\)
vậy hệ có nghiệm duy nhất \(x=-y=-\frac{7}{4}\)

`#3107.101107`
`D = x^3 - y^3 - 3xy` biết `x - y - 1 = 0`
Ta có:
`x - y - 1 = 0`
`=> x - y = 1`
`D = x^3 - y^3 - 3xy`
`= (x - y)(x^2 + xy + y^2) - 3xy`
`= 1 * (x^2 + xy + y^2) - 3xy`
`= x^2+ xy + y^2 - 3xy`
`= x^2 - 2xy + y^2`
`= x^2 - 2*x*y + y^2`
`= (x - y)^2`
`= 1^2 = 1`
Vậy, với `x - y = 1` thì `D = 1`
________
`E = x^3 + y^3` với `x + y = 5; x^2 + y^2 = 17`
`x + y = 5`
`=> (x + y)^2 = 25`
`=> x^2 + 2xy + y^2 = 25`
`=> 2xy = 25 - (x^2 + y^2)`
`=> 2xy = 25 - 17`
`=> 2xy = 8`
`=> xy = 4`
Ta có:
`E = x^3 + y^3`
`= (x + y)(x^2 - xy + y^2)`
`= 5 * [ (x^2 + y^2) - xy]`
`= 5 * (17 - 4)`
`= 5 * 13`
`= 65`
Vậy, với `x + y = 5; x^2 + y^2 = 17` thì `E = 65`
________
`F = x^3 - y^3` với `x - y = 4; x^2 + y^2 = 26`
Ta có:
`x - y = 4`
`=> (x - y)^2 = 16`
`=> x^2 - 2xy + y^2 = 16`
`=> (x^2 + y^2) - 2xy = 16`
`=> 2xy = (x^2 + y^2) - 16`
`=> 2xy = 26 - 16`
`=> 2xy = 10`
`=> xy = 5`
Ta có:
`F = x^3 - y^3`
`= (x - y)(x^2 + xy + y^2)`
`= 4 * [ (x^2 + y^2) + xy]`
`= 4 * (26 + 5)`
`= 4*31`
`= 124`
Vậy, với `x - y = 4; x^2 + y^2 = 26` thì `F = 124.`

a) Ta thấy \(xy=\dfrac{\left(x+y\right)^2-\left(x^2+y^2\right)}{2}=\dfrac{3^2-5}{2}=2\)
\(\Rightarrow x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)\) \(=3\left(5-2\right)=9\)
b) Ta thấy \(xy=\dfrac{-\left(x-y\right)^2+\left(x^2+y^2\right)}{2}=\dfrac{15-5^2}{2}=-5\)
\(\Rightarrow x^3-y^3=\left(x-y\right)\left(x^2+y^2+xy\right)\) \(=5\left(15-5\right)=50\)

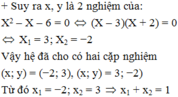

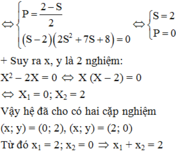

\(x^3-16x=y\left(y^2-4\right)\) \(\left(1\right)\)
\(5x^2=y^2-4\) \(\left(2\right)\)
\(\Rightarrow x^3-16x=y.5x^2\Leftrightarrow x\left(x^2-5yx-16\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(x^2-5yx-16=0\)
+ \(x=0\Rightarrow y^2-4=5.0=0\Rightarrow y=2\) hoặc \(y=-2\)
Thế lại vào \(\left(1\right)\) thấy thỏa, ta được 2 nghiệm \(\left(x,y\right)=\left(0;2\right),\left(0;-2\right)\)
+\(x^2-5yx-16=0\) và \(x\ne0\)
\(\Rightarrow y=\frac{x^2-16}{5x}=\frac{x}{5}-\frac{16}{5x}\)
Thế y vào \(\left(2\right)\) ta được
\(5x^2=\left(\frac{x}{5}-\frac{16}{5x}\right)^2-4\Leftrightarrow125x^2=\left(x-\frac{16}{x}\right)^2-100\Leftrightarrow125x^2=x^2+\frac{256}{x^2}-32-100\)
\(\Leftrightarrow124x^2+132-\frac{256}{x^2}=0\)\(\Leftrightarrow124x^4+132x^2-256=0\)
\(\Leftrightarrow4\left(x^2-1\right)\left(31x^2+64\right)=0\)\(\Leftrightarrow x^2=1\Leftrightarrow x=1\) hoặc \(x=-1\)
\(x=1\Rightarrow y=\frac{1}{5}-\frac{16}{1.5}=-3\)
\(x=-1\Rightarrow y=\frac{1}{-5}-\frac{16}{-5}=3\)
Thử các cặp \(\left(x,y\right)=\left(1;-3\right),\left(-1;3\right)\) vào hệ thấy thỏa mãn.
Vậy: hệ có 4 nghiệm \(\left(x,y\right)=\left(0;2\right),\left(0;-2\right);\left(1;-3\right);\left(-1;3\right)\)