Tìm số tự nhiên \(x\) sao cho biểu thức P=(\(x\)-1)(\(x^2\)-\(x\)+1) có giá trị là một số nguyên tố.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
23 tháng 2 2022
Lời giải:
a. Để A là số nguyên tố thì 1 trong 2 thừa số $x-2, x+4$ có giá trị bằng 1 và số còn lại là số nguyên tố.
Mà $x-2< x+4$ nên $x-2=1$
$\Rightarrow x=3$
Thay vào $A$ thì $A=7$ là snt (thỏa mãn)
b. Để $A<0\Leftrightarrow (x-2)(x+4)<0$
Điều này xảy ra khi $x-2,x+4$ trái dấu. Mà $x-2< x+4$ nên:
$x-2<0< x+4$
$\Rightarrow -4< x< 2$
$x$ nguyên nên $x=-3,-2,-1,0,1$
LH
1
1 tháng 5 2019
Ta phải tìm số tự nhiên n để P = (n - 1)(n2- n + 1) là số nguyên tố .
P = (n - 1)(n2- n + 1) là một tích , P là số nguyên tố thì P chỉ có 2 ước số là 1 và chính nó. Như vậy P = (n - 1)(n2- n + 1) là số nguyên tố thì:
\(\orbr{\begin{cases}\hept{\begin{cases}n-1=1\\p=n^2-n+1\end{cases}}\\\hept{\begin{cases}n^2-n+1=1\\p=n-1\end{cases}}\end{cases}}\)- T rường hợp 1; n - 1 = 1 , tức là n = 2 khi đó p = n2 - n + 1 = 3 thỏa mãn
- Trường hơp 2 : n2 - n + 1 = 1 , ta tìm được n = 0 , n = 1 . Cả hai giá trị này đều cho ta số p = n - 1 không phải là số nguyên tố.
Trả lời n = 2 , p = 3
HX
4
9 tháng 10 2017
Xét \(x=0\)
\(\Rightarrow M=1\)không phải số nguyên tố.
Xét \(x>0\) thì ta có:
\(M=x^{1999}+x^{1997}+1=\left(x^{1999}-x\right)+\left(x^{1997}-x^2\right)+x^2+x+1\)
\(=x\left(\left(x^3\right)^{666}-1\right)+\left(\left(x^3\right)^{665}-1\right)+x^2+x+1\)
\(=\left(x^2+x+1\right)A+\left(x^2+x+1\right)B+x^2+x+1\)
\(=\left(x^2+x+1\right)C\)
Vì M là số nguyên tố nên nó có 2 ước là 1 và chính nó. Ta lại thấy \(x^2+x+1>1\)
\(\Rightarrow x^{1999}+x^{1997}+1=x^2+x+1\)
\(\Leftrightarrow\left(x^{1999}-x^2\right)+\left(x^{1997}-x\right)=0\)
Ta có: \(\hept{\begin{cases}x^{1999}-x^2\ge0\\x^{1997}-x\ge0\end{cases}}\)
Dấu = xảy ra khi \(x=1\)
9 tháng 10 2017
Ta có : M=x1999+x1997+1=x(x1998−1)+x2(x1995−1)+x2+x+1=BS(x2+x+1)x1999+x1997+1=x(x1998−1)+x2(x1995−1)+x2+x+1=BS(x2+x+1)
Do đó , để M là số nguyên tố ⇔M=x2+x+1⇔M=x2+x+1
⇔x=1
KV
27 tháng 10 2023
a) 2ˣ + 2ˣ⁺³ = 72
2ˣ.(1 + 2³) = 72
2ˣ.9 = 72
2ˣ = 72 : 9
2ˣ = 8
2ˣ = 2³
x = 3
b) Để số đã cho là số nguyên thì (x - 2) ⋮ (x + 1)
Ta có:
x - 2 = x + 1 - 3
Để (x - 2) ⋮ (x + 1) thì 3 ⋮ (x + 1)
⇒ x + 1 ∈ Ư(3) = {-3; -1; 1; 3}
⇒ x ∈ {-4; -2; 0; 2}
Vậy x ∈ {-4; -2; 0; 2} thì số đã cho là số nguyên
c) P = |2x + 7| + 2/5
Ta có:
|2x + 7| ≥ 0 với mọi x ∈ R
|2x + 7| + 2/5 ≥ 2/5 với mọi x ∈ R
Vậy GTNN của P là 2/5 khi x = -7/2
15 tháng 12 2023
1: \(D=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{x^2-16}\)
\(=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{x-4+x\left(x+4\right)+24-x^2}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{-x^2+x+20+x^2+4x}{\left(x+4\right)\left(x-4\right)}=\dfrac{5x+20}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{5\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5}{x-4}\)
2: Khi x=10 thì \(D=\dfrac{5}{10-4}=\dfrac{5}{6}\)
3: \(M=\left(x-2\right)\cdot D=\dfrac{5\left(x-2\right)}{x-4}\)
Để M là số nguyên thì \(5\cdot\left(x-2\right)⋮x-4\)
=>\(5\left(x-4+2\right)⋮x-4\)
=>\(5\left(x-4\right)+10⋮x-4\)
=>\(10⋮x-4\)
=>\(x-4\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
=>\(x\in\left\{5;3;6;2;9;-1;14;-6\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 1 2021
\(P=x^4+2x^2+1-x^2=\left(x^2+1\right)^2-x^2\)
\(P=\left(x^2-x+1\right)\left(x^2+x+1\right)\)
\(\Rightarrow\) P luôn có ít nhất 2 ước số là \(x^2-x+1\) và \(x^2+x+1\)
Do \(x^2+x+1\ge x^2-x+1\) nên P là SNT khi và chỉ khi \(x^2-x+1=1\) đồng thời \(x^2+x+1\) là SNT
\(x^2-x+1=1\Leftrightarrow x^2-x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
- Với \(x=0\Rightarrow x^2+x+1=1\) ko phải SNT (loại)
- Với \(x=1\Rightarrow x^2+x+1=3\) là SNT (t/m)
Vậy \(x=1\)
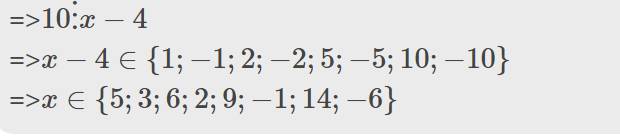
`P= (x-1)(x^2-x+1)` là một số nguyên tố
`=>` \(\left[{}\begin{matrix}x-1=1\\x^2-x+1=1\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=2\\x=0\\x=1\end{matrix}\right.\)