Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc ADB=góc DAC+góc ACD
=>góc ADB>góc ACD
=>góc ADB>góc ABD
=>AB>AD
Vì ΔABC cân tại A
nên góc ACB<90 độ
=>góc ACE>90 đô
=>AE>AC=AB
=>AD<AC<AE

BÀI NÀY MÌNH KO CHÈN ĐƯỢC HÌNH MONG BẠN THÔNG CẢM !!!
a. Xét tứ giác AEDF có: AF // DE
AE // DF
\(\Rightarrow\) AEDF là hình bình hành
\(\Rightarrow\)AD cắt EF tại trung điểm mỗi đường.
Mà O là giao của AD và EF
\(\Rightarrow\) O là trung điểm AD
Mà \(\Delta AHD\) vuông tại H
\(\Rightarrow\) HO = AO
Do đó \(\Delta AOH\) cân tại O

https://lazi.vn/edu/exercise/cho-tam-giac-abc-co-goc-a-120-do-duong-phan-giac-ad-d-thuoc-bc-ve-de-vuong-goc-voi-ab-df-vuong-goc
a) ΔAED=ΔAFDΔAED=ΔAFD(ch-gn)nên DE=DF.(hai cạnh tương ứng)
Mặt khác dễ dàng chứng minh được EDFˆ=60o
Vì vậy tam giác DEF là tam giác đều
b)ΔEDK=ΔFDT(hai cạnh góc vuông)
nen DK=DI(hai cạnh tương ứng).Do đó Tam giác DIK cân ở D
c) AD là tia phân giác của góc BAC nên DAB^=DAC^=1/2BAC^=60o
AD//MC(gt),do đó AMCˆ=DABˆ=60o(hai góc nằm trong vị trí đồng vị)
AMC^=CAD^=60o(hai góc nằm trong vị trí sole trong)
Tam giác AMC có hai góc bằng nhau và khoảng 60o nên là tam giác đều
d)Ta có AF=AC-FC=CM-FC=m-n.

DA*DP=DB*DC
=>DA/DC=DB/DP
=>ΔDAB đồng dạng với ΔDCP
=>góc BAD=góc PCD
=>ABPC nội tiếp

a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).

đừng xem chùa T_T
ủng hộ tôi bằng cách liike ik mờ
a, Vì △ABC cân tại A => AB = AC và ABC = ACB
Xét △ABD và △ACE
Có: AB = AC (cmt)
ABD = ACE (cmt)
BD = CE(gt)
=> △ABD = △ACE (c.g.c)
b, Xét △AHD vuông tại H và △AIE vuông tại I
Có: AD = AE (△ABD = △ACE)
HAD = IAE (△ABD = △ACE)
=> △AHD = △AIE (ch-gn)
=> HD = IE (2 cạnh tương ứng)
c, Xét △AHI có: AH = AI (△AHD = △AIE) => △AHI cân tại A => AHI = (180o - HAI) : 2 (1)
Vì △ABC cân tại A => ABC = (180o - BAC) : 2 (2)
Từ (1) và (2) => AHI = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> HI // BC (dhnb)
d, Gọi { O } = HD
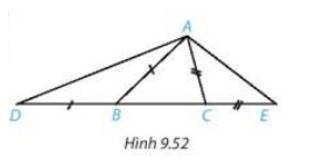
góc ADB=góc DAC+góc ACD
=>góc ADB>góc ACD
=>góc ADB>góc ABD
=>AB>AD
Vì ΔABC cân tại A
nên góc ACB<90 độ
=>góc ACE>90 đô
=>AE>AC=AB
=>AD<AC<AE