cho đường tròn o r và điểm m nằm ngoài đường tròn .qua m kẻ hai tiếp tuyến ma,mb với đường tròn (0,r) (a,b là tiếp điểm ) đoạn thẳng om cắt đường thẳng ab tại điểm h và cắt đường tròn (0,r) tại I 1, chứng minh M,A,B,O cùng thuộc một đường tròn 2,kẻ đường kính A,B của đường tròn (O,R) Đoạn thẳng MD cắt đường tròn (O,R) tại C khác D chứng minh MA² =MH.MO=MC.MD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2023
1: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
2: góc ACD=1/2*sđ cung AD=90 độ
ΔMAD vuông tại A có AC là đường cao
nên MA^2=MC*MD
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
=>MH*MO=MA^2=MC*MD
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Lời giải:
1.
Vì $MA, MB$ là tiếp tuyến của $(O)$ nên:
$MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Tứ giác $MAOB$ có tổng 2 góc đối nhau $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
$\Rightarrow M, A, O,B$ cùng thuộc 1 đường tròn.
2.
Vì $MA=MB, OA=OB$ nên $MO$ là trung trực cuả $AB$
$\Rightarrow MO\per AB$ tại $H$
Xét tam giác $AMO$ vuông tại $A$ có đường cao $AH$. Áp dụng hệ thức lượng trong tgv thì:
$MA^2=MH.MO$
Xét tam giác $MCB$ và $MBD$ có:
$\widehat{M}$ chung
$\widehat{MBC}=\widehat{MDB}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn cung đó)
$\Rightarrow \triangle MCB\sim \triangle MBD$ (g.g)
$\Rightarrow \frac{MC}{MB}=\frac{MB}{MD}$
$\Rightarrow MC.MD=MB^2$
Mà $MB^2=MA^2\Rightarrow MA^2=MH.MO=MC.MD$ (đpcm)
6 tháng 12 2023
a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b; Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB
CM
4 tháng 1 2017
Đáp án A
Ta có: OA = OB = R nên tam giác ABO là cân tại O (1)
Theo tính chất hai tiếp tuyến cắt nhau ta có: OH là tia phân giác của góc AOB (2)
Từ (1) và (2) suy ra: OH là đường cao trong tam giác AOB hay OH ⊥ Ab.
* Xét tam giác vuông AOM có :
CM
16 tháng 6 2018
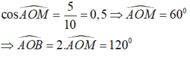
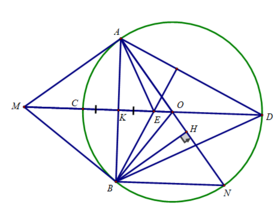
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB
5 tháng 3 2021
a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: M,A,O,B cùng thuộc một đường tròn(đpcm)
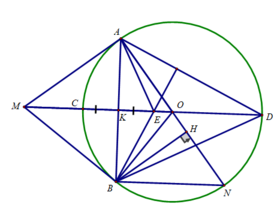
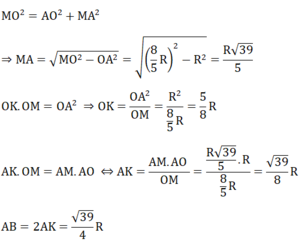
Đề là đường kính AD hay sao nhỉ?
Mình làm tắt nha bạn không hiểu đâu thì hỏi lại nhé
a) MA, MB là tiếp tuyến
=> \(\widehat{OBM}=\widehat{OAM}=90^o\) (t/c tiếp tuyến)
=> \(\widehat{OBM}+\widehat{OAM}=180^o\)
mà 2 góc đối nhau
=> tứ giác AOBM nội tiếp
=> 4 điểm A, O, B, M cùng thuộc 1 đường tròn
b) Áp dụng hệ thức lượng vào tam giác OAM vuông tại A đường cao AH
=> \(AM^2=MH.MO\)
Áp dụng hệ thức lượng vào tam giác DAM vuông tại A đường cao AC
=> \(AM^2=MC.MD\)
=> \(AM^2=MH.MO=MC.MD\)