:. Cho nửa đường tròn (O), đường kính AB = 2R. Gọi Ax, By là các tia vuông góc với AB (Các tia Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm I thuộc nửa đường tròn (I khác A và B) kẻ tiếp tuyến với nửa đường tròn (O), nó cắt các tia Ax, By lần lượt ở M và N. a) Chứng minh:góc MON=90 độ b) Chứng minh : MN = AM + BN. c) Chứng minh AB là tiếp tuyến của đường tròn...
Đọc tiếp
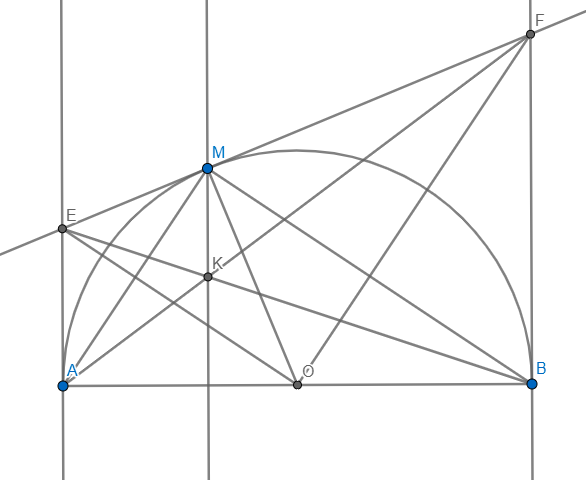
:. Cho nửa đường tròn (O), đường kính AB = 2R. Gọi Ax, By là các tia vuông góc với AB (Các tia Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm I thuộc nửa đường tròn (I khác A và B) kẻ tiếp tuyến với nửa đường tròn (O), nó cắt các tia Ax, By lần lượt ở M và N.
a) Chứng minh:góc MON=90 độ
b) Chứng minh : MN = AM + BN.
c) Chứng minh AB là tiếp tuyến của đường tròn đường kính MN.
d) Xác định vị trí của điểm I trên nửa đường tròn (O) để diện tích tứ giác AMNB đạt giá trị nhỏ nhất.
a: Xét (O) có
MI,MA là tiếp tuyến
nên MI=MA và OM là phân giác của góc AOI(1)
Xét (O) có
NI,NB là tiếp tuyến
nên NI=NB và ON là phân giác của góc IOB(2)
Từ (1), (2) suy ra góc MON=1/2*180=90 độ
b: MN=MI+IN
=>MN=MA+NB
c: Gọi H là trung điểm của MN
Xét hình thang AMNB có
O,H lần lượt là trung điểm của AB,MN
nên HO là đường trung bình
=>HO//AM//BN
=>HO vuông góc AB
=>AB là tiếp tuyến của(H)