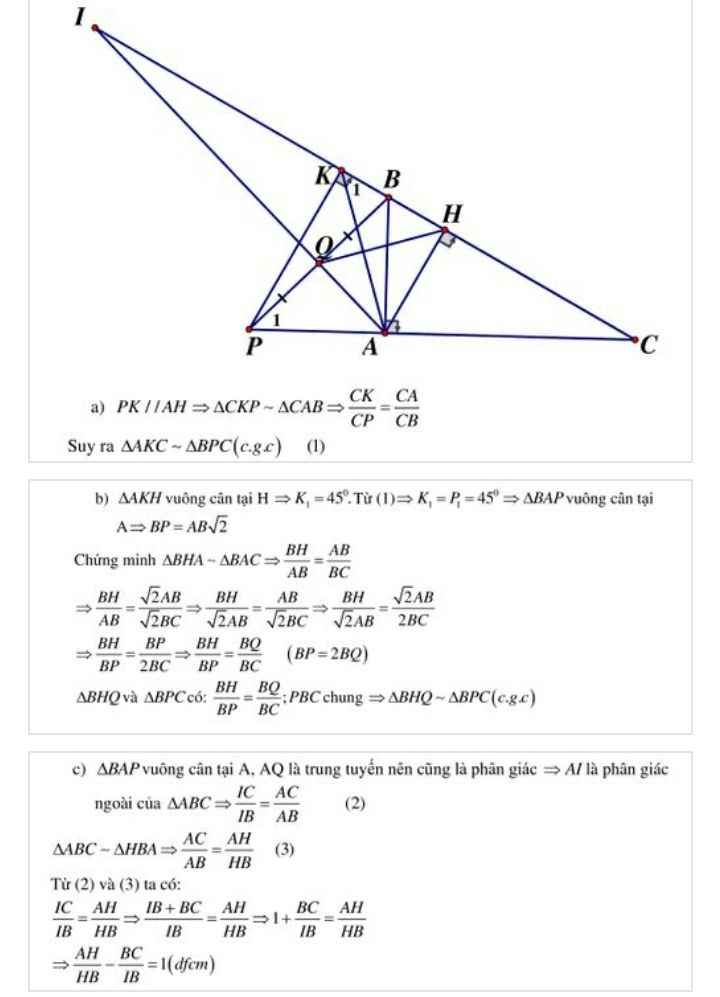
Cho tam giác ABC vuông tại A (AC > AB)đường cao AH ( H € BC ). Trên tia đối của tia bc lấy điểm K sao cho HK = HA qua K kẻ đường thẳng song song với AC cắt đường thẳng AC tại P a) Cm ∆ ABC ~ ∆ KPC b) Gọi Q là trung điểm của BP. Cm QA=QK và QH vuông góc AK c)Cm góc AKC = góc BPC d)Cm BP.HQ = BH.PC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 10 2020
a) 2 tâm giác vuông có 1 góc nhọn bằng nhau
b) QK=QA suy ra dpcm
10 tháng 1
Xét tứ giác ABDC có
AB//DC
AC//BD
Do đó: ABDC là hình bình hành
=>AD cắt BC tại trung điểm của mỗi đường
=>K là trung điểm chung của AD và BC
Xét ΔAED có
H,K lần lượt là trung điểm của AE,AD
=>HK là đường trung bình của ΔAED
=>HK//ED
Ta có: HK//ED
HK\(\perp\)AE
Do đó: ED\(\perp\)AE
=>ΔAED vuông tại E
Ta có: ΔEAD vuông tại E
mà EK là đường trung tuyến
nên KE=KD
=>ΔKED cân tại K
1 tháng 8 2019
a) Xét ∆ADC có :
CH là trung tuyến AD ( AH = HD )
CH là đường cao
=> ∆ADC cân tại C
=> CH là phân giác DCA
Hay CB là phân giác DCA
b) Xét ∆ vuông BHA và ∆ vuông DHE ta có :
BHA = DHE
HA = HD
=> ∆BHA = ∆DHE (cgv-gn)
=> BAH = HDE
Mà 2 góc này ở vị trí so le trong
=> BA//DE
c) Chứng minh DKA = 90°
=> HK = HD = HA ( tính chất )
=> HK = \(\frac{1}{2}\:AD\)
Giúp mình đi mai mik nộp r