Cho tam giác ABC thỏa mãn điều kiện \(\widehat{A}=2\widehat{B}=4\widehat{C}\)
Chứng minh rằng: \(\dfrac{1}{AB}=\dfrac{1}{AC}+\dfrac{1}{BC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình gửi kèm
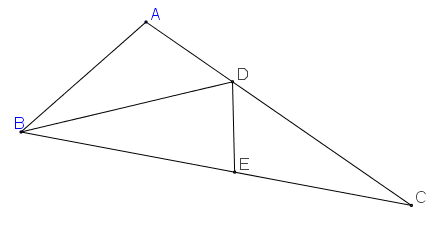 Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/
Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/

Dễ dàng c/m : \(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}=1\)
Ta có : \(\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le\dfrac{1}{a+b+4}\le\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}\right)\)
Suy ra : \(\Sigma\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le2.\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}\right)=\dfrac{1}{2}.1=\dfrac{1}{2}\)
" = " \(\Leftrightarrow a=b=c=1\)

a: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*CB
=>AB^2/AC^2=BH/CH
b:
góc B=90-60=30 độ
góc HAB=90-30=60 độ
BC=căn 8^2+12^2=4*căn 13(cm)
HB=AB^2/BC=36/căn 13(cm)
AH=8*12/4*căn 13=24/căn 13(cm)