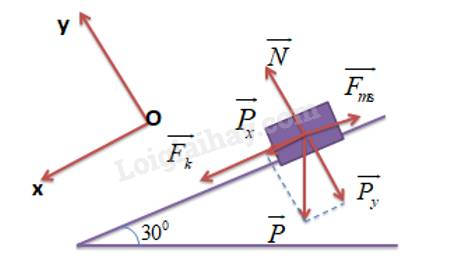
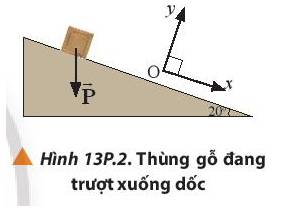
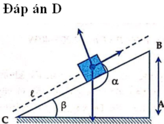
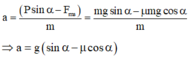Một thùng hàng trọng lượng 500 N đang trượt xuống dốc. Mặt dốc tạo với phương ngang một góc 30,00. Chọn hệ tọa độ vuông góc xOy sao cho trục Ox theo hướng chuyển động của thùng.
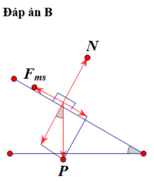
a) Vẽ giản đồ vectơ lực tác dụng lên thùng.
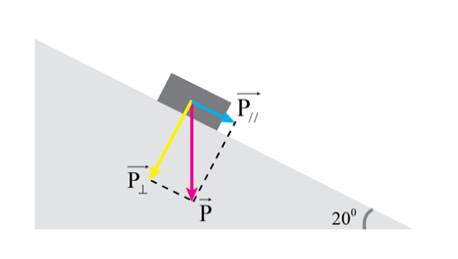
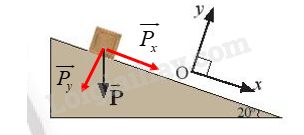
b) Tính các thành phần của trọng lực theo các trục tọa độ vuông góc.
c) Giải thích tại sao lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc.
d) Xác định hệ số ma sát trượt giữa mặt dốc và thùng hàng nếu đo được gia tốc chuyển động của thùng là 2,00m/s2. Bỏ qua lực cản của không khí lên thùng.