Cho nửa đường tròn (O) đường kính AB. Vẽ 2 tiếp tuyến Ax; By (Ax; By cùng nằm trên nửa mặt phẳng bờ AB). Qua M bất kỳ trên (O) (M khác A,B) kẻ tiếp tuyến thứ 3 cắt Ax, By theo thứ tự C,D. Gọi N là giao điểm của AD và BC.
a) Chứng minh A,C,M,O cùng thuộc một đường tròn
b) Chứng minh AC. BD không đổi khi M di chuyển trên (O)
c) Chứng minh MN ⊥ AB
d) Chứng minh MN= OC^2.OD^2/ CD^3
giúp mk vs! mk đang cần gấp

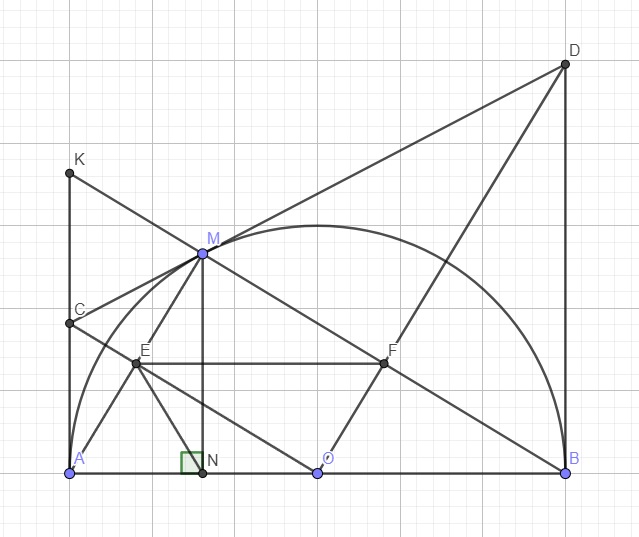
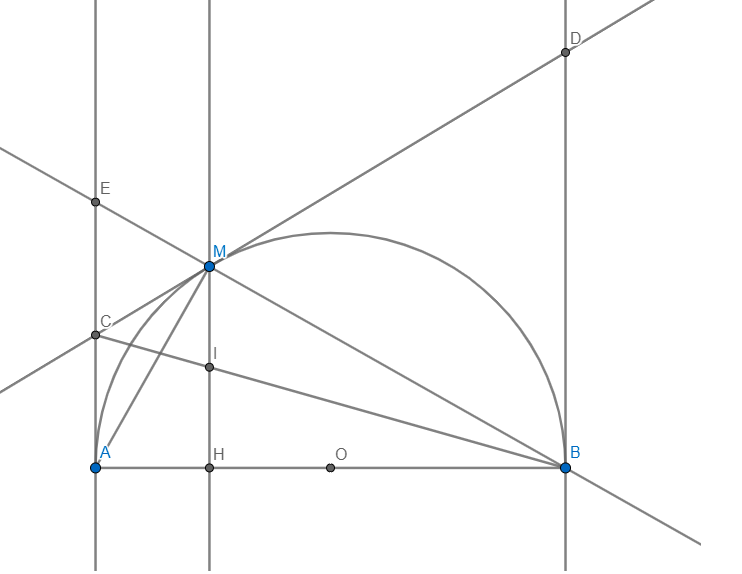
Gợi ý:
a) Có \(A,M\) cùng nhìn \(CO\) dưới góc \(90^o\) nên \(A,C,M,O\) cùng thuộc một đường tròn.
b) \(CA=CM,DB=DM\) (tính chất hai tiếp tuyến cắt nhau)
Xét tam giác \(COD\) vuông tại \(O\) đường cao \(OM\):
\(OM^2=CM.DM=AC.BD\).
c) Kẻ \(MH\perp AB\). Kéo dài \(BM\) cắt \(Ax\) tại \(E\).
Tam giác \(AME\) vuông tại \(M\) có \(CM=CA\) do đó \(C\) là trung điểm của \(AE\).
Suy ra \(BC\) đi qua trung điểm của \(MH\).
Tương tự ta cũng chứng minh được \(AD\) đi qua trung điểm của \(MH\).
Vậy \(M,N,H\) thẳng hàng suy ra \(MN\perp AB\).
d) Ta có \(\dfrac{OC^2.OD^2}{CD^3}=\dfrac{\left(OC.OD\right)^2}{CD^3}=\dfrac{\left(OM.CD\right)^2}{CD^3}=\dfrac{OM^2}{CD}\).
\(\dfrac{DM}{DC}=\dfrac{MN}{AC},\dfrac{CM}{DC}=\dfrac{MN}{BD}\) suy ra \(\dfrac{DM+CM}{DC}=MN\left(\dfrac{1}{AC}+\dfrac{1}{BD}\right)\)
\(\Leftrightarrow MN=\dfrac{AC.BD}{AC+BD}=\dfrac{OM^2}{CD}\).
Suy ra đpcm.