Một người viết ngẫu nhiên một số tự nhiên có bốn chữ số. Tính xác xuất để các chữ số của một số được viết ra có thứ tự giảm dần.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 1
a: Số cách viết ngẫu nhiên một số tự nhiên có 2 chữ số là:
99-10+1=90(số)
b: Số số chẵn có 2 chữ số là: \(\dfrac{98-10}{2}+1=\dfrac{88}{2}+1=45\left(số\right)\)
=>Xác suất viết được một số chẵn là \(\dfrac{45}{90}=\dfrac{1}{2}\)
Số số tròn chục có 2 chữ số là: \(\dfrac{90-10}{10}+1=9\left(số\right)\)
=>Xác suất viết ra được một số tròn chục là \(\dfrac{9}{90}=\dfrac{1}{10}\)
Các số có 2 chữ số mà là bình phương của một số tự nhiên là 16;25;36;49;64;81
=>Có 6 số
=>Xác suất viết được là 6/90=1/15
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Tập hợp C gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra là:
C = {10; 11; 12; …; 97; 98; 99}
Số phần tử của C là 90.
a) Có chín kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số chia hết cho cả 2 và 5” là: 10, 20, 30, 40, 50, 60, 70, 80, 90.
Vì thế, xác suất của biến cố trên là: \(\dfrac{9}{{90}} = \dfrac{1}{{10}}\)
b) Có năm kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số có tổng các chữ số bằng 5” là: 14, 23, 32, 41, 50.
Vì thế, xác suất của biến cố trên là: \(\dfrac{5}{{90}} = \dfrac{1}{{18}}\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Tập hợp D gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra là:
D = {10; 11; 12; …; 97; 98; 99}
Số phần tử của D là 90
a) Có sáu kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là bình phương của một số tự nhiên” là: 16, 25, 36, 49, 64, 81.
Vì thế, xác suất của biến cố trên là: \(\dfrac{6}{{90}} = \dfrac{1}{{15}}\)
b) Có sáu kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là bội của 15” là: 15, 30, 45, 60, 75, 90.
Vì thế, xác suất của biến cố trên là: \(\dfrac{6}{{90}} = \dfrac{1}{{15}}\)
c) Có tám kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là ước của 120” là: 10, 12, 15, 20, 24, 30, 40, 60.
Vì thế, xác suất của biến cố trên là: \(\dfrac{{8}}{{90}} = \dfrac{4}{45}\)
12 tháng 5 2023
a: D={10;11;...;99}
=>n(D)=99-10+1=90
A={16;25;36;49;64;81}
=>n(A)=6
=>P=6/90=1/15
b: B={15;30;45;60;75;90}
=>P(B)=6/90=1/15
c: C={10;12;15;20;30;40;60}
=>n(C)=7
=>P(C)=7/90
CM
12 tháng 1 2018
Chọn A
Xét phép thử: “Chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có bốn chữ số”
Ta có 
Biến cố A: “Số được chọn có ít nhất hai chữ số 8 đứng liền nhau”.
Gọi số có 4 chữ số a b c d ¯ là trong đó có ít nhất hai chữ số 8 đứng liền nhau, a ≠ 0
TH1: Có đúng hai chữ số 8 đứng liền nhau.
+) Số có dạng 88 c d ¯ : có 9.9 = 81 số.
+) Số có dạng a 88 d ¯ hoặc a b 88 ¯ : mỗi dạng có 8.9 = 72 số.
TH2: Có đúng ba chữ số 8 trong đó có ít nhất hai chữ số 8 đứng liền nhau.
+) Số có dạng a 888 ¯ : có 8 số.
+) Số có dạng 8 b 88 ¯ hoặc 88 c 8 ¯ hoặc 888 d ¯ : Mỗi dạng có 9 số.
TH3: Cả 4 chữ số đều là chữ số 8: Có 1 số là số 8888
Do đó n(A) = 81 + 2.72 + 8 + 3.9 + 1 = 261
Xác suất cần tìm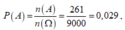 
Không gian mẫu: \(9.10.10.10=9000\)
Số cách viết thỏa mãn: \(C_{10}^4=210\)
Xác suất: \(P=\dfrac{210}{9000}=...\)