Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔCAB có CF/CA=CE/CB
nên FE//AB và FE=AB/2
=>FE//AD và FE=AD
Xét tứ giác AFED có
FE//AD
FE=AD
góc FAD=90 độ
Do đó: AFED là hình chữ nhật
Xét tứ giác AECK có
F là trung điểm chung của AC và EK
EA=EC
Do đó: AECK là hình thoi
b: \(S_{ABC}=\dfrac{1}{2}\cdot4\cdot5=10\left(cm^2\right)\)
Bài 1:
a) Xét tam giác ABC vuông tại A có:
+ D là trung điểm của AB (gt).
+ E là trung điểm của AC (gt).
=> DE là đường trung bình (Định nghĩa đường trung bình trong tam giác).
=> DE = \(\dfrac{1}{2}\)BC (Tính chất đường trung bình trong tam giác).
Mà BC = 10 cm (gt).
=> DE = 5 cm.
Vậy DE = 5 cm.
b) Xét tam giác ABC vuông tại A có:
DE là đường trung bình (cmt)
=> DE // BC (Tính chất đường trung bình trong tam giác).
Ta có: F là trung điểm của BC (gt). => BF = CF = \(\dfrac{1}{2}\)BC.
Mà DE = \(\dfrac{1}{2}\)BC (cmt).
=> BF = CF = DE = \(\dfrac{1}{2}\)BC.
Xét tứ giác BDEF có:
+ BF = DE (cmt).
+ BF // DE (do DE // BC).
=> Tứ giác BDEF là hình bình hành (dhnb).
c) Xét tam giác ABC vuông tại A:
+ D là trung điểm của AB (gt).
+ F là trung điểm của BC (gt).
=> DF là đường trung bình (Định nghĩa đường trung bình trong tam giác).
=> DF // AC và DF = \(\dfrac{1}{2}\)AC (Tính chất đường trung bình trong tam giác).
Ta có: DF = \(\dfrac{1}{2}\)AC (cmt).
Mà AE = CE = \(\dfrac{1}{2}\)AC (E là trung điểm AC).
=> AE = CE = DF = \(\dfrac{1}{2}\)AC.
Xét tứ giác ADEF có:
+ AE = DF (cmt).
+ AE // DF (do DF // AC).
=> Tứ giác ADEF là hình bình hành (dhnb).
Mà ^DAE = 90o (do tam giác ABC vuông tại A).
=> Tứ giác ADEF là hình chữ nhật (dhnb).
d) Gọi I là giao điểm của AF và DE.
Xét hình chữ nhật ADEF có: I là giao điểm của AF và DE (cách vẽ).
=> I là trung điểm của AF và DE (Tính chất hình chữ nhật). (1)
Ta có: G là điểm đối xứng của F qua D (gt).
=> D là trung điểm của CG.
=> DF = \(\dfrac{1}{2}\)GF.
Mà DF = \(\dfrac{1}{2}\)AC (cmt).
=> GF = AC.
Xét tứ giác GACF có:
+ GF = AC (cmt).
+ GF // AC (do DF // AC).
=> Tứ giác GACF là hình bình hành (dhnb).
=> Giao điểm của 2 đường chéo AF và GC là trung điểm mỗi đường (Tính chất hình bình hành).
Mà I là trung điểm của AF (cmt)
=> I là trung điểm của GC (2).
Từ (1) và (2) => Các đường thẳng AF; GC; DE cùng cắt nhau tại điểm I.
hay các đường thẳng AF; GC; DE cùng cắt nhau tại trung điểm mỗi đường (đpcm).
a: Xét ΔABC có
BE/BC=BD/BA
nên ED//AC và ED=AC/2
=>ED//AF và ED=AF
=>ADEF là hình bình hành
mà góc FAD=90 độ
nên ADEF là hình chữ nhật
b: Xét tứ giác BMAE có
D là trung điểm chung của BA vàME
EA=EB
Do đó: BMAE là hình thoi
c: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
S=1/2*3*4=6(cm2)
Tứ giác AEDF là hình chữ nhật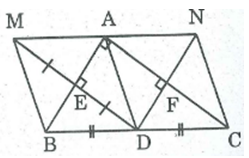
⇒ DE // AC; DF // AB
Trong ∆ ABC, ta có: DB = DC (gt)
Mà DE // AC
Suy ra: AE = EB (tính chất đường trung bình của tam giác)
Lại có: DF // AB và DB = DC
Suy ra: AF = FC (tính chất đường trung bình của tam giác)
Xét tứ giác ADBM, ta có: AE = EB (cmt)
ED = EM (vì AB là trung trực DM)
Suy ra tứ giác ADBM là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mặt khác: AB ⊥ DM
Vậy hình bình hành ADBM là hình thoi (vì có hai đường chéo vuông góc)
Xét tứ giác ADCN, ta có: AF = FC (cmt)
DF = FN (vì AC là đường trung trực DN)
Suy ra tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Lại có: AC ⊥ DN
Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo cắt nhau)
a: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
b: AC=8cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\cdot6}{2}=24\left(cm^2\right)\)
c: Ta có: D và E đối xứng nhau qua AB
nên AD=AE
=>ΔADE cân tại A
mà AB là đường trung trực
nên AB là tia phân giác của góc DAE(1)
Ta có: D và F đối xứng nhau qua AC
nên AC là đường trung trực của DF
=>AD=AF
=>ΔADF cân tại A
mà AC là đường trung trực của DF
nên AC là tia phân giác của góc DAF(2)
Từ (1) và (2) suy ra \(\widehat{FAE}=2\cdot\left(\widehat{BAD}+\widehat{CAD}\right)=2\cdot90^0=180^0\)
Do đó: F,A,E thẳng hàng
Mình vẽ hình hơi xâu, bạn thông cảm nhé!
a) Xét từ giác ABMC có: + AM cắt BC tại D (bạn dùng ký hiệu giao nhé)
+ DA = DM (gt)
+ DB = DM(gt)
suy ra, tứ giác AMCM là hình bình hành mà ta có góc CAB là góc vuông suy ra tứ giác ABMC là hình chữ nhật
Các câu còn lại bạn đầu có thể giải theo cách trên nhé!
( e mk chưa làm đc, mk mới đc học đến bào hình chữ nhật thôi, sory)
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
a: Xét ΔCAB có CF/CA=CE/CB
nên FE//AB và FE=AB/2
=>FE//AD và FE=AD
Xét tứ giác AFED có
FE//AD
FE=AD
góc FAD=90 độ
Do đó: AFED là hình chữ nhật
Xét tứ giác AECK có
F là trung điểm chung của AC và EK
EA=EC
Do đó: AECK là hình thoi
b: \(S_{ABC}=\dfrac{1}{2}\cdot4\cdot5=10\left(cm^2\right)\)