Cho tam giác DEF vuông tại D có điểm M là trung điểm của EF.Gọi N là điểm đối xứng của D qua M a) Chứng minh tứ giác DENF là hình chữ nhật b) Biết DE = 3cm, DF =4cm hãy tính độ dài của DM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 1 2022
a: EF=5cm
DM=2,5cm
b: Xét tứ giác DENF có
M là trung điểm của EF
M là trung điểm của DN
Do đó: DENF là hình bình hành
mà \(\widehat{EDF}=90^0\)
nên DENF là hình chữ nhật
c: Xét tứ giác FBEA có
FB//EA
FB=EA
Do đó: FBEA là hình bình hành
Suy ra: Hai đường chéo FE và BA cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của FE
nên M là trung điểm của BA
hay M,A,B thẳng hàng
23 tháng 12 2021
a/ Xét tứ giác DPMQ có
∠EDF=∠MQD=ˆMPD=90oEDF^=MQD^=MPD^=90o
=> Tứ giác DPMQ là hcn
b/ Để hcn DPMQ là hình vuông thì DM là tia pg ^EDF
c/ Có I đx M qua DE
=> DE là đường t/trực của IM
=> DI = DM (1)
=> t/g DIM cân tại D có DE là đường trung trực
=> DE đồng thời là đường pg
=> ˆIDE=ˆEDMIDE^=EDM^ (2)
CMTT : DM = DK (3) ; ˆKDF=ˆFDMKDF^=FDM^ (4)
Từ (2) ; (4)
=> ∠IDE+∠EDF+∠KDF=∠IDK=180oIDE^+EDF^+KDF^=IDK^=180o
=> I,D,K thẳng hàng
Từ (1) ; (3)=> ID = DK
Do đó D là trđ IK
=> I đx K qua D
7 tháng 8 2019
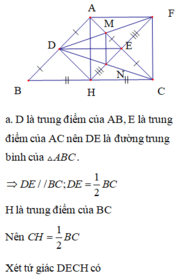
a, Ta có: DE//BC \(\Rightarrow\widehat{DEB}+\widehat{EBF}=180\)
mà góc EBF =90 => góc DEB =90 (1)
Chứng minh tương tự với DF//AB
\(\Rightarrow\widehat{EDF}=90;\widehat{BFD}=90\) (2)
Từ (1) và (2) => tứ giác BEDF là hình chữ nhật
DT
7 tháng 8 2019
a) vì ED//BC và DF//AB
Mà \(\Delta ABC\)vuông tại B
Nên \(DE\perp AB\)và \(DF\perp BC\)
Xét tứ giác BEDF có:
\(\widehat{B}=\widehat{DEB}=\widehat{DFB}=90^0\)
Vậy tứ giác BEDF là hình chữ nhật
8 tháng 1 2022
1: BC=5cm
Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình
=>DM=AC/2=2(cm)
2: Xét tứ giác ACME có
ME//AC
ME=AC
Do đó: ACME là hình bình hành
Xét tứ giác AEBM có
D là trung điểm của ME
D là trung điểm của AB
Do đó: AEBM là hình bình hành
mà MA=MB
nên AEBM là hình thoi
a) Xét $\Delta DME$ và $\Delta NMF$ có:
$EM = MF$ ($M$ là trung điểm của $EF$);
$DM = MN$ ($N$ đối xứng với D qua $M$);
$\widehat{EMD} = \widehat{NMF}$ (hai góc đối đỉnh);
Suy ra $\Delta DME$ và $\Delta NMF$ (c.g.c).
Suy ra $DE = NF$
và $DE$ // $NF$ (do hai góc so le trong $\widehat{MED}$ và $\widehat{MFN}$ bằng nhau).
Do đó $DENF$ là hình bình hành, có một góc vuông nên $DENF$ là hình chữ nhật em nhé.
b) Xét tam giác $DEF$ vuông tại $D$ có:
$DE^2 + DF^2 = EF^2$ suy ra $EF = 5$ cm;
Mà $DM = \dfrac12 DN$ và $DN = EF$ nên $DM = 2,5$ cm.