Viết biểu thức sau dưới dạng lũy thừa với a là cơ số: a2+a4:a2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 7 2021
Bài 1:
a) \(4^8\cdot2^{20}=\left(2^2\right)^8\cdot2^{20}=2^{36}\)
\(64^3\cdot4^5=\left(2^6\right)^3\cdot\left(2^2\right)^5=2^{18}\cdot2^{10}=2^{28}\)
\(y\cdot y^7=y^{1+7}=y^8\)
\(a^n\cdot a^2=a^{n+2}\)
14 tháng 7 2021
Bài 1:
b) \(10^8:2^8=5^8\)
\(17^8:17^5=17^3\)
\(2^{25}:32^4=2^{25}:2^{20}=2^5\)
\(19^4:9^4=\left(\dfrac{19}{9}\right)^4\)
14 tháng 10 2022
`2^5 . 8^4 = 2^5 . (2^3)^4 = 2^5 . 2^12 = 2^17`
`25^6 . 125^3 = (5^2)^6 . (5^3)^3 = 5^12 . 5^9 = 5^21`
`625^5 : 25^7 = (5^4)^7 : (5^2)^7 = 5^28 : 5^14 = 5^14`
`12^3 . 3^3 = (12 . 3)^3 = 36^3`
NT
2
MF
26 tháng 10 2017
A=1+3+3^2+...+3^99
3A=3+3^2+3^3+...+3^100
3A-A=3^100-1
2A=3^100-1
A=(3^100-1):2
mik chỉ làm được đến đó thôi
26 tháng 10 2017
A=1+3+3^2+...+3^99
3A=3+3^2+3^3+...+3^100
3A-A=2A=3^100-1
\(\Rightarrow\)2A+1=3^100
Khong viet dc vi 3^100 le ma 4^n chan
NT
1
26 tháng 10 2017
ta có : \(A=1+3+3^2+...+3^{99}\)
\(\Rightarrow3A=3\left(1+3+3^2+...+3^{99}\right)\)
\(\Leftrightarrow3A=3+3^2+3^3+...+3^{100}\)
\(\Rightarrow3A-A=2A=\left(3+3^2+3^3+...+3^{100}\right)-\left(1+3+3^2+...+3^{99}\right)\)
\(\Leftrightarrow2A=3^{100}-1\)
\(\Rightarrow2A+1=3^{100}-1+1=3^{100}=\left(3^{25}\right)^4\)
vậy \(2A+1=\left(3^{25}\right)^4\)
CM
20 tháng 11 2019
Đáp án C
Ta có 2 2 .2 1 2 .8 = 2 2 .2 1 2 .2 3 = 2 2 + 1 2 + 3 = 2 11 2
PT
1
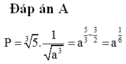
a^2 + a^4 : a^2 = a^2 + a^ (4-2) =a^2 +a^2 =2a^2
a^2 + a^4 : a^2 = a^2 + a^ (4-2) =a^2 +a^2 =2a^2