Cho hàm số y=(m-1).x+3
a) tìm m để đồ thi hàm số đi qua A(-1;2)
b) tìm m để đồ thị hàm số cắt trục tung tại điểm có tọa độ là -2
c) tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ là -1
Làm giúp mk vs mk like hết cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
8 tháng 8 2023
a)
để đồ thị hàm số đi qua điểm `A(1;-1)`
`<=>-1=(m+1)*1-3`
`<=>m+1-3=-1`
`<=>m-2=-1`
`<=>m=1`
Vậy m=1 thì đồ thị hàm số đi qua điểm `A(1;-1)`
b)
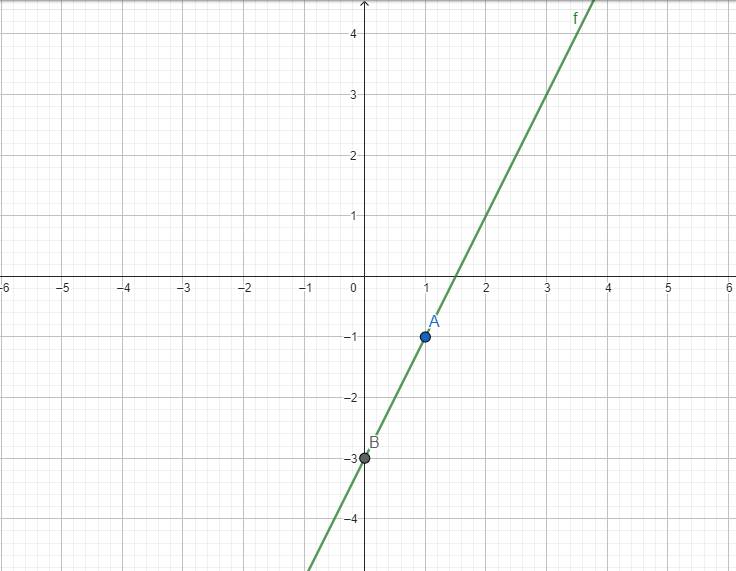
Với `m=1` khi đó `y=(1+1)*x-3<=>y=2x-3`
Với `x=0=>y=2*0-3=-3`
=> điểm `B(0;-3)` thuộc đồ thị hàm số `y=2x-3`
8 tháng 8 2023
a) Để đồ thị hàm số đi qua điểm A(1;-1), ta thay x = 1 và y = -1 vào phương trình của hàm số:
-1 = (m+1)(1) - 3
-1 = m + 1 - 3
-1 = m - 2
m = 1
Vậy, với giá trị m = 1, đồ thị hàm số sẽ đi qua điểm A(1;-1).
b) Đồ thị của hàm số y = (m+1)x - 3 sẽ là một đường thẳng.
22 tháng 12 2023
a: Thay x=1 và y=-1 vào (d), ta được:
\(\left(m-2\right)\cdot1+m+1=-1\)
=>m-2+m+1=-1
=>2m-1=-1
=>2m=0
=>m=0
b: Thay y=0 vào y=x+2, ta được:
x+2=0
=>x=-2
Thay x=-2 và y=0 vào y=(m-2)x+m+1, ta được:
-2(m-2)+m+1=0
=>-2m+4+m+1=0
=>5-m=0
=>m=5
AH
Akai Haruma
Giáo viên
23 tháng 12 2021
Lời giải:
a. Với $m=3$ thì ptđt là $y=-x+3$. Đồ thị $y=-x+3$ như dưới đây:
b. Để hàm số đồng biến thì: $2-m>0$
$\Leftrightarrow m< 2$
c. Để đths đi qua $M(-1;1)$ thì $y_M=(2-m)x_M+3$
$\Leftrightarrow 1=(2-m)(-1)+3$
$\Leftrightarrow m=0$
d. Để đths đã cho với $y=-x+2$ song song với nhau thì:
$2-m=-1$
$\Leftrightarrow m=3$
AH
Akai Haruma
Giáo viên
9 tháng 12 2023
Lời giải:
a. Để hàm đồng biến thì $m-1>0\Leftrightarrow m>1$
Để hàm nghịch biến thì $m-1<0\Leftrightarrow m< 1$
b. Để đths đi qua điểm $A(-1;1)$ thì:
$y_A=(m-1)x_A+m$
$\Leftrightarrow 1=(m-1)(-1)+m=1-m+m$
$\Leftrightarrow 1=1$ (luôn đúng)
Vậy đths luôn đi qua điểm A với mọi $m$
c.
$x-2y=1\Rightarrow y=\frac{1}{2}x-\frac{1}{2}$
Để đths đã cho song song với đths $y=\frac{1}{2}x-\frac{1}{2}$ thì:
\(\left\{\begin{matrix} m-1=\frac{1}{2}\\ m\neq \frac{-1}{2}\end{matrix}\right.\Leftrightarrow m=\frac{3}{2}\)
d,
ĐTHS cắt trục hoành tại điểm có hoành độ $\frac{2-\sqrt{3}}{2}$, tức là ĐTHS đi qua điểm $(\frac{2-\sqrt{3}}{2}; 0)$
$\Rightarrow 0=(m-1).\frac{2-\sqrt{3}}{2}+m$
$\Leftrightarrow m=\frac{2-\sqrt{3}}{4-\sqrt{3}}$
22 tháng 11 2021
\(a,\Leftrightarrow2m-2+m+3=4\Leftrightarrow m=1\\ b,\text{Gọi điểm cố định mà (1) luôn đi qua là }A\left(x_0;y_0\right)\\ \Leftrightarrow y_0=\left(m-1\right)x_0+m+3\\ \Leftrightarrow mx_0-x_0+m+3-y_0=0\\ \Leftrightarrow m\left(x_0+1\right)+\left(3-x_0-y_0\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0+1=0\\3-x_0-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=4\end{matrix}\right.\Leftrightarrow A\left(-1;4\right)\)
Vậy (1) luôn đi qua A(-1;4)
13 tháng 1 2021
a. Để hs (1) đồng biến trên R :
\(\Leftrightarrow-m-18>0\)
\(\Leftrightarrow-m>18\)
\(\Leftrightarrow m< -18\)
Vậy \(m< -18\) thì hs (1) đồng biến trên R
b. Do ĐTHS (1) // đ.t \(y=-19x-5\) nên :
\(\left\{{}\begin{matrix}-m-18=-19\\3m+1\ne-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m\ne-2\end{matrix}\right.\)
c. Vì ĐTHS (1) đi qua điểm \(A\left(-1;2\right)\) nên ta có : x = -1 và y = 2
Thay x = -1 và y = 2 vào (1) ta được :
\(2=\left(-m-18\right).\left(-1\right)+3m+1\)
\(\Leftrightarrow2=m+18+3m+1\)
\(\Leftrightarrow-17=4m\)
\(\Leftrightarrow m=\dfrac{-17}{4}\)
N
13 tháng 1 2021
a. hàm số (1) đồng biến trên R khi -m-18 > 0 <=> m < -18 . Vậy m < -18 thì hàm số (1) đồng biến. b. đồ thị hàm số (1) song song với đường thẳng y= -19x-5 <=> -m-18=-19 và 3m+1 khác -5 <=> m= 1 và m khác 4/3 . Vậy m=1 và m khác 4/3 thì đồ thị hàm số ( 1 ) song song với đường thẳng y= -19x-5 . c. đồ thị hàm số y=(-m-18)x+3m+1 đi qua A(-1;2) => x=-1 ; y=2 => 2=(-m-18)*(-1)+3m+1 <=> 2= m+18+3m+1 <=> 4m=17 <=> m=17/4 . Vậy m=17/4 thì đồ thị hàm số y=(-m-18)x+3m+1 đi qua A(-1;2)
Y
7 tháng 8 2023
\(y=\left(m^2-9\right)x+8m\left(1\right)\)
\(a,A\left(0;8\right)\in y=\left(m^2-9\right)x+8m\)
\(\Rightarrow x=0;y=8\)
Thay \(x=0;y=8\) vào \(\left(1\right)\), ta được : \(8=\left(m^2-9\right).0+8m\Rightarrow8m=8\Rightarrow m=1\)
\(b,\) Hàm số trên nghịch biến \(\Leftrightarrow a< 0\Leftrightarrow m^2-9< 0\Leftrightarrow\left(m-3\right)\left(m+3\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m-3< 0\\m+3>0\end{matrix}\right.\\\left\{{}\begin{matrix}m-3>0\\m+3< 0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m< 3\\m>-3\end{matrix}\right.\\\left\{{}\begin{matrix}m>3\\m< -3\end{matrix}\right.\end{matrix}\right.\)
\(c,\) Hàm số trên qua \(B\left(x_B;y_B\right)\) có hoành độ = 1 \(\Rightarrow x_B=1,y_B=0\)
\(\Rightarrow0=\left(m^2-9\right).1+8.1\Rightarrow m^2-9+8=0\Rightarrow m^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-1\\m=1\end{matrix}\right.\)
7 tháng 8 2023
Mình xin phép sửa lại câu b của bạn Thư một chút nha:
b: Để hàm số nghịch biến thì m^2-9<0
=>(m-3)(m+3)<0
=>-3<m<3